【深層学習】ニューラルネットワークの仕組みとディープラーニングモデル性能最適化のポイント解説

2022年3月5日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

本記事はディープラーニングの実装を検討している方向けです。深層学習モデルを実装するための仕組みとモデルを最適化する手法など重要なポイントを踏襲しています。本記事読了後、モデル改善に向けた適切なアプローチができるようになるでしょう。

ディープラーニング概要

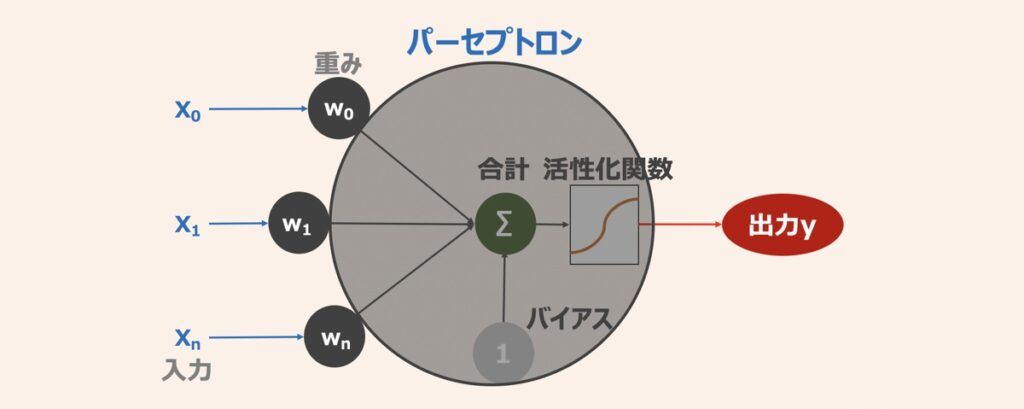
ディープラーニングはニューラルネットワークを多層化した機械学習手法であり、ニューラルネットワークは上図のようなパーセプトロン(ニューロン)の相互接続によって構成されます。パーセプトロンの挙動を解説すると、まず複数の入力が重みと掛け合わされた後、総和をとります。続いて活性化関数で処理され出力が得られる仕組みです。

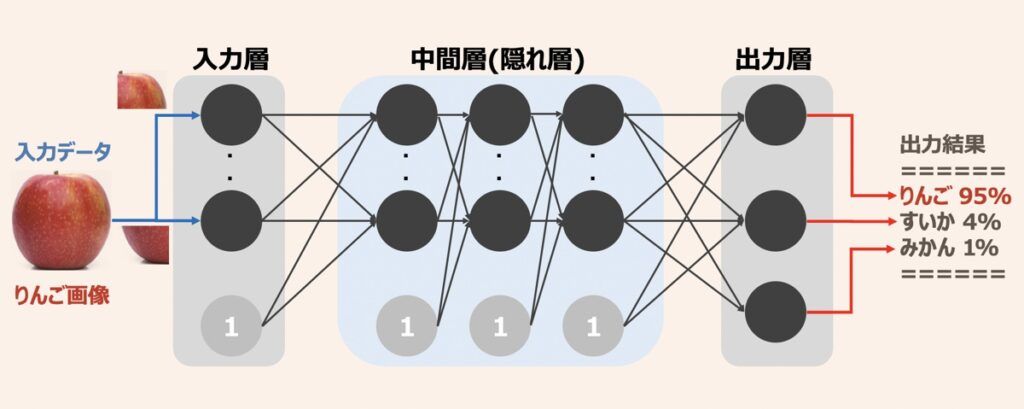
パーセプトロンを多数の層で相互接続させるとニューラルネットワークが構築できます。ここで中間層(隠れ層)は入力層と出力層の間にある複数の層を指します。ニューラルネットワークの中間層をさらに多層化することでディープニューラルネットワークが完成します。

「そもそもディープラーニングとは何か？」詳しく知りたい方は下記の入門記事をご覧ください。

合わせて読みたい

ディープラーニング・Pythonプログラミングを学ぶ上でおすすめの教材は下記で紹介しています。

【Python・深層学習入門】おすすめの本・動画教材7選

ディープラーニングの学習プロセス

ディープラーニングにおける学習では、得られた出力結果を正解ラベルと比較し、出力と正解の誤差を算出します。そして「誤差が最小となるようパラメータ(重みやバイアス等)を調整していく」のが特徴的な学習プロセスになります。この学習手法は「誤差伝播法」と呼ばれます。ディープラーニングを実装し精度最適化に取り組む方は、この手法は必ず理解することを推奨します。

後述ではまずディープラーニングの学習プロセスで大切な概念である「順伝播」と「逆伝播」について解説し、モデル性能が最適化されていく仕組みを解説します。

順伝播

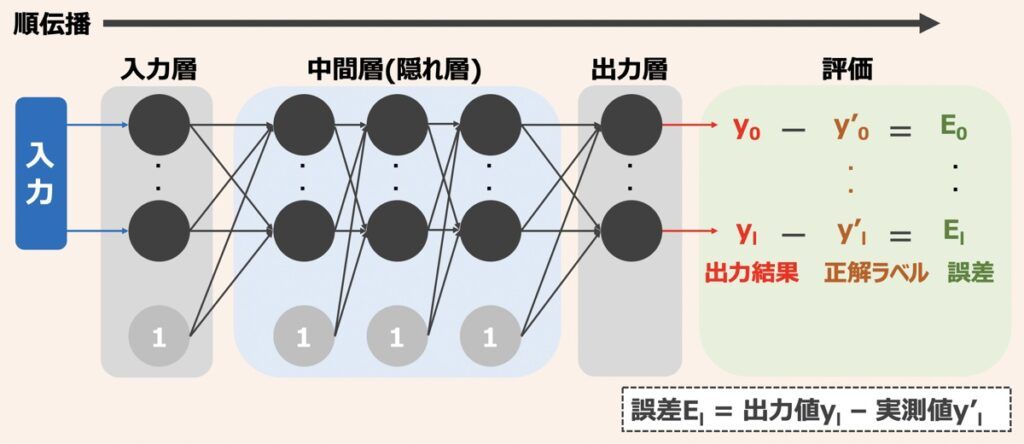
ニューラルネットワーク入出力の演算プロセスについて解説します。入力層がネットワーク外の入力を受け取り、出力層がネットワーク内で演算された結果を出力します。ここで、入力層は単に受け取った入力を中間層に渡すのみで、実際にパーセプトロンの演算が実行されるのは、中間層と出力層になります。

このように入力層から出力層にかけて、入力値→途中結果の演算値→出力結果が伝播する流れを「順伝播」と言います。ニューラルネットワークにおいて予測や分類問題を扱う際は、この順伝播を利用します。

誤差逆伝播法(バックプロパケーション)

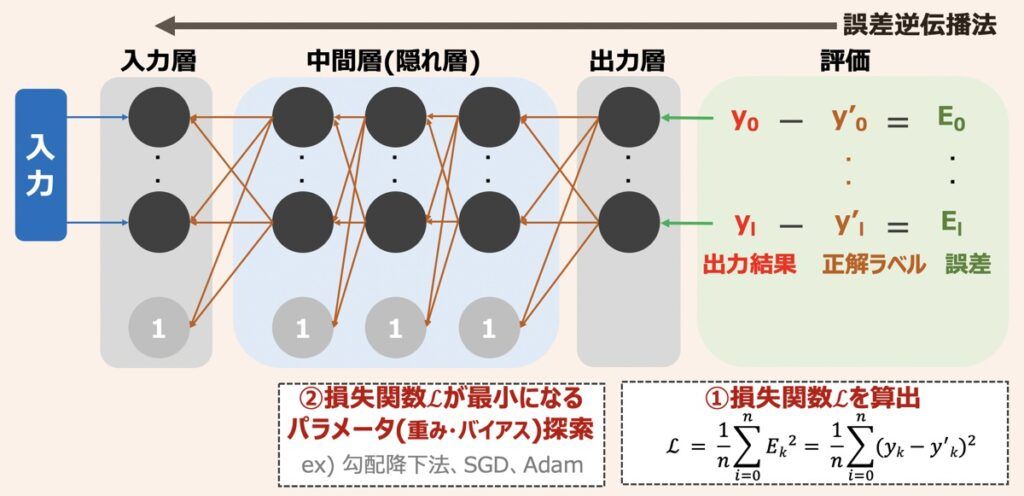
ニューラルネットワークモデルが構築された初期の状態は、パラメーターがでたらめに設定されているため、出力結果も正確ではありません。そのため、ニューラルネットワークにおいても従来の教師あり機械学習アルゴリズムのように、学習データを用いたモデル学習が必要となります。ニューラルネットワークにおける代表的な学習手法は、上図で示した「誤差逆伝播法」に該当します。

誤差逆伝播法とは「ニューラルネットワークの出力結果と正解ラベルの差である誤差が、出力層から入力層へ逆伝播するようパラメータを再演算することで、誤差を最小化できるパラメータを見つけ出すという一連の学習手法」を指します。具体的に、出力結果と正解ラベルの誤差の総和である「損失関数」を算出し、その値が小さくなるようにパラメータを調整していきます。損失関数の概要については後述します。

ニューラルネットワーク最適化の仕組み

機械学習やニューラルネットワークのモデル学習は「最適化する」とも呼ばれます。後述ではニューラルネットワークモデルを最適化する際に必ず押さえるべきポイントを徹底解説します。以下が本記事でカバーする範囲です。これらを把握することで、モデル最適化問題における具体的なアプローチが設計できるようになります。

損失関数と勾配降下法：パラメータ探索アルゴリズムの選定とチューニング
活性化関数の選定
学習データの投入方法
学習回数(エポック数)
学習・テストデータの分割
ドロップアウト
正則化
内部共変量シフトとBatch Normalization

損失関数と勾配降下法

ニューラルネットワークモデルを最適化するとは、出力結果と正解ラベルの誤差の総和である「損失関数」を最小化できるようなパラメータ(重みやバイアス等)を探し出すことです。損失関数はモデルの出力がどれだけ正解とずれているかを表す指標であり、数式は下記のように示されます。

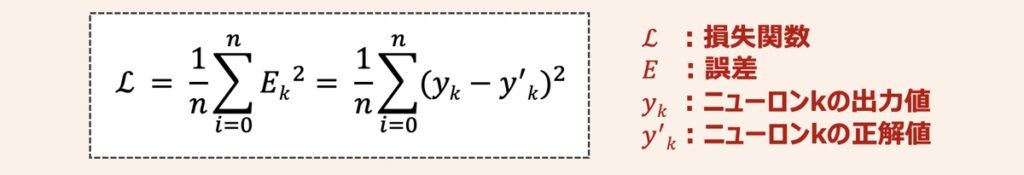
損失関数・パラメータ値を用いてグラフを描画すると下記のように表せます。

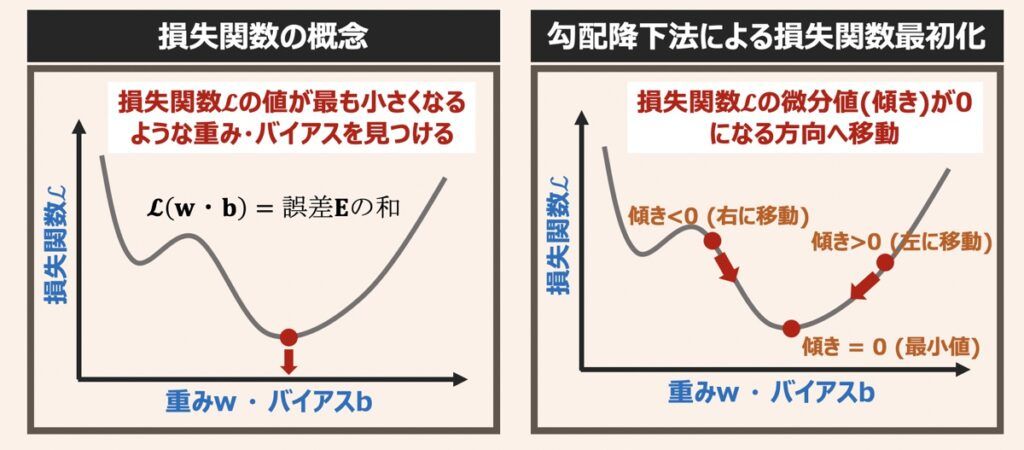
ニューラルネットワークモデルの最適化は、損失関数の最小値をとりうるパラメータ組み合わせを探すアルゴリズムを用いて行われます。そのため、「損失関数を最小化するパラメータ探索アルゴリズムの選定とそのアルゴリズム独自で用いられるパラメーターのチューニング」が最適化観点で重要です。

代表的なパラメータ探索アルゴリズムとして「勾配降下法」があります。勾配降下法を一言で例えると「損失関数という山(グラフ形状)を勾配(傾き)の降る方向に降りていき、勾配が平な場所(損失関数の最小値)に着地する方法」と言えます。勾配降下法による損失関数を最小化する仕組みや探索アルゴリズムの役割については下記の記事で解説しています。パラメータ探索アルゴリズムの選定やチューニングパラメーターの理解を促す内容も含まれているため是非ご覧ください。

活性化関数の選定

活性化関数は入力を重み付けした合計値を別の値に変換する数式であり、ディープラーニングの予測性能に寄与する関数です。活性化関数を用いることで、最終的に柔軟な出力結果を算出できるようになります。そのため、ニューラルネットワーク最適化問題を扱う上で「適切な活性化関数の選定」は重要です。

活性化関数はグラフ上で一直線でない非線形関数が用いられるのが特徴です。直近よく用いられる関数はReLU関数です。ReLUを用いる理由はニューラルネットワーク特有の消失問題が起きにくいためです。消失問題の詳細は下記記事で紹介しているため適時ご参照ください。

学習データの投入方法

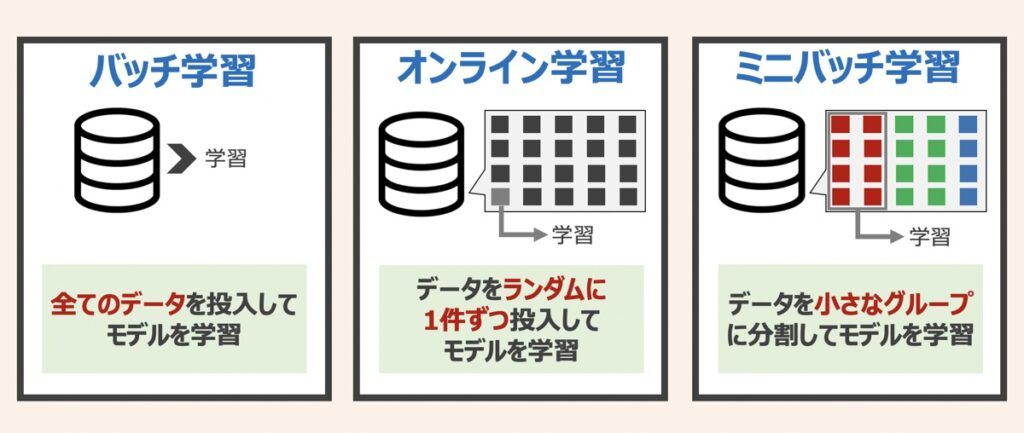
ニューラルネットワークは、学習データを損失関数に投入して誤差が最小となるようにパラメータを調整します。ニューラルネットワーク最適化において「学習データの投入方法」の検討も大切な要素です。上図に示した「バッチ学習」「オンライン学習」「ミニバッチ学習」という3つの投入方法があります。それぞれの詳細は下記記事で解説していますため、是非ご覧ください。

ディープラーニングにおいては、現在「ミニバッチ学習」が広く採用されています。IoTやビッグデータの普及に伴い、扱えるデータ量が増大しているため、バッチ学習はメモリサイズの逼迫により現実的でないケースが多くなっています。また、データを1件ずつ扱うオンライン学習は計算速度も遅い傾向にあるためです。

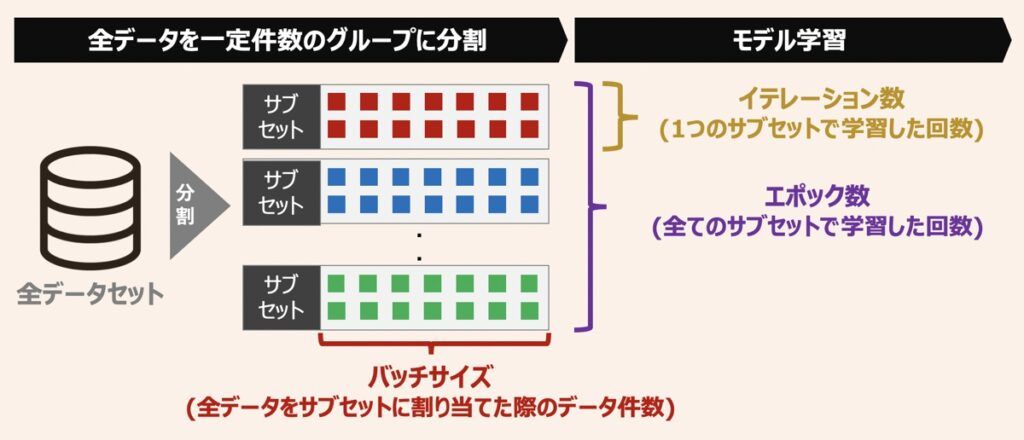
上図にミニバッチ学習における概略図を示します。ニューラルネットワークモデルの最適化を検討する上では、ミニバッチ学習を利用し、なるべく大きなバッチサイズを設定することが一般的です。

学習回数(エポック数)

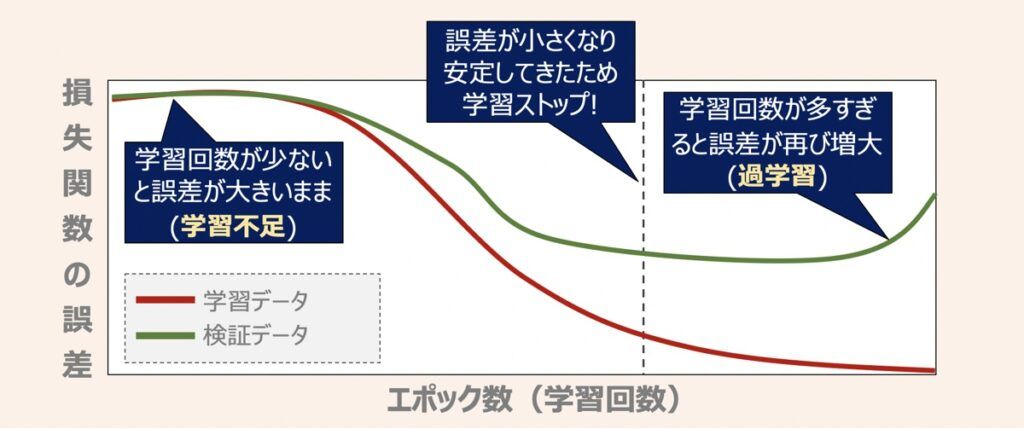
最適化観点では「学習回数」も大切な要素です。上述したミニバッチ学習を適用して学習を繰り返した際の誤差の変化を上図に示します。ここで、エポック数とは学習回数を表す単位であり、1つの学習データセットを何回繰り返し学習するかを表した数です。

エポック数を多く設定すると学習に時間がかかる一方、モデルの性能は改善できます。しかしエポック数を多く設定しすぎると、学習用データに対する性能は向上する一方で、未知のデータに対する予測性能(汎化性能)は低くなるという過学習の状態に陥ります。実装の場面では、モデルの性能が安定するまでエポック数を増やしていき、安定した段階で学習を止めるEarly Stoppingという手法が広く採用されています。

学習・テストデータの分割

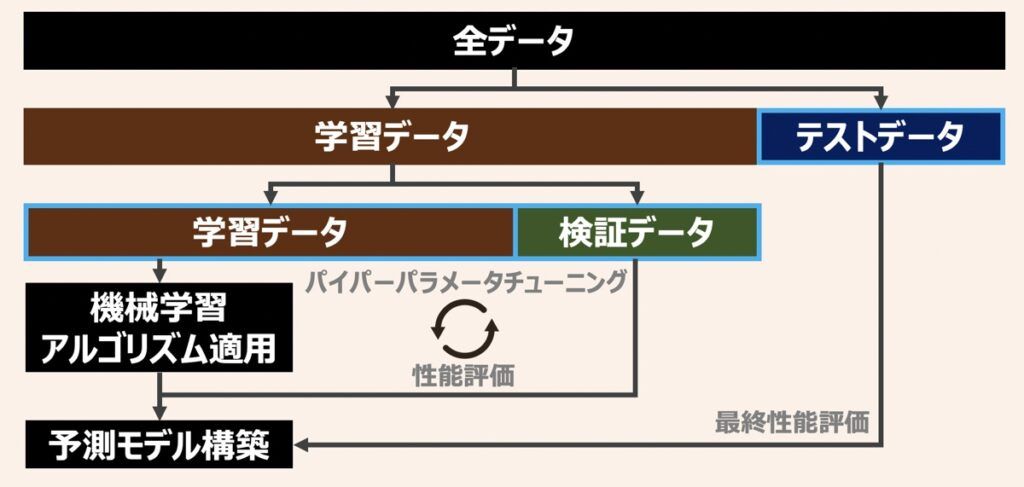
ディープラーニングだけでなく機械学習モデルを構築する際に共通して重要なのは、データを学習して未知のデータの予測を行えるようにすることです。この未知のデータに対する予測精度を汎化性能と呼びます。

モデル学習は、学習データを基準にパラメータを更新して、学習データ内に限った予測性能向上を目指している段階であるため、その時点で汎化性能は保証されていません。汎化性能を正確に評価するには、全てのデータセットを学習データとして使うのではなく、学習データ・検証データ・テストデータに分割して使用するのが好ましいと言えます。各データの役割は下記になります。

データ	役割
学習データ	モデルを学習するために用いる
検証データ	学習データを構築したモデルから誤差を評価するために用いるハイパーパラメータの最適化や、過学習の兆候発見が主な目的
テストデータ	全ての学習過程が終わったタイミングでモデルの汎化性能の評価で用いる

学習データと検証データの利用

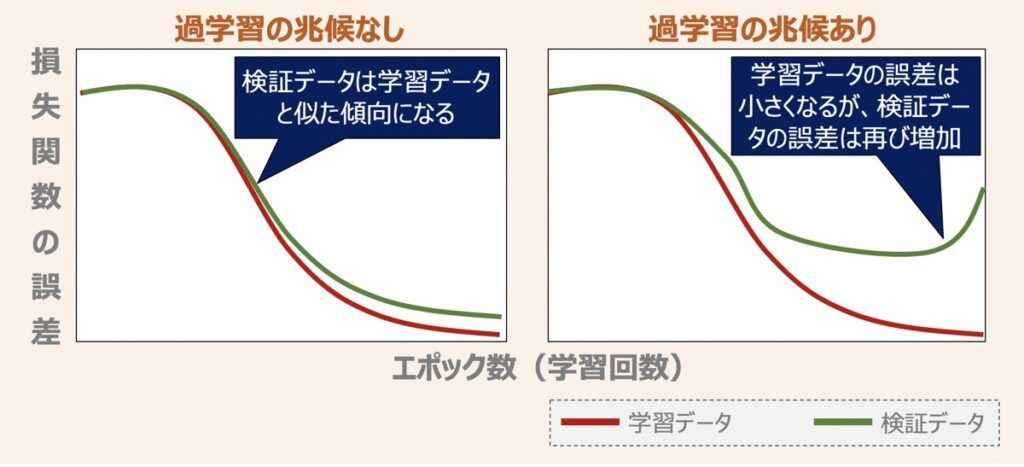
ここで深層学習における検証データの使われ方について少し触れます。検証データは主にハイパーパラメータを最適化するために用いられます。さらには、パラメータ最適化の過程で発現しうる過学習対策としても有用です。上図に過学習の兆候有無で出力されるグラフの傾向を示しました。過学習対策として「検証データの誤差が安定した段階で学習を終了させる」という使い方をします。

データの分割による汎化性能の検証方法

学習データ・検証データ・テストデータを用いた代表的な検証方法として「ホールドアウト検証」と「K分割交差検証(k-fold cross validation)」があります。これら2つの分割方法の詳細は下記の記事で紹介していますのでぜひご覧ください。

ドロップアウト(Drop Out)

ドロップアウトとはモデルの性能向上のために、過学習を抑える目的で導入される手法です。ニューラルネットワークで扱うパラメーターが多くなると、学習に大量のデータが必要になると同時に、過学習も起こりやすくなります。ドロップアウトは、上図に示すような逆伝播のモデル学習時に、一定の割合でランダムに一部のユニットを無視することを指します。全てのユニットを学習に用いないことで過学習を抑制するのです。

多層化した複雑なニューラルネットワークではドロップアウトを設定しないと過学習の兆候が現れやすくなってしまいます。一方でドロップアウトの割合が高すぎると、過学習を防止できるものの学習自体が進まなくなってしまいます。モデルの最適化という観点ではドロップアウトの適切な割合を指定することが大切です。

正則化

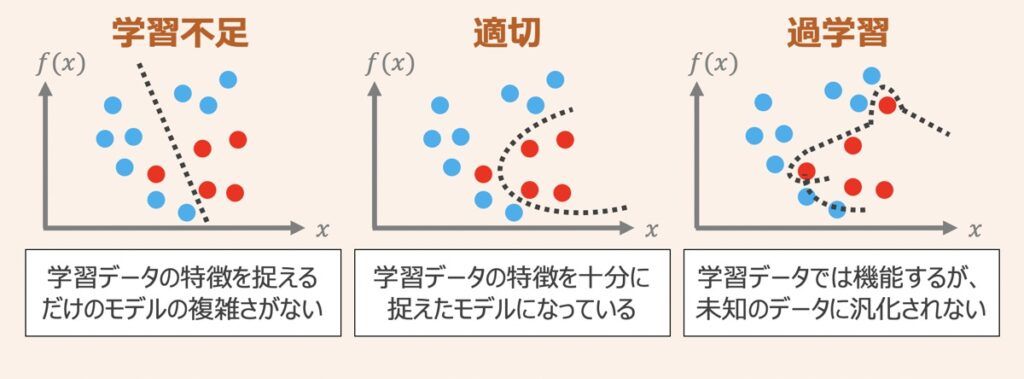
正則化とは過学習を抑制することを目的とした手法であり、パラメータ(重み)にペナルティを科すための追加情報(バイアス)を導入することを指します。

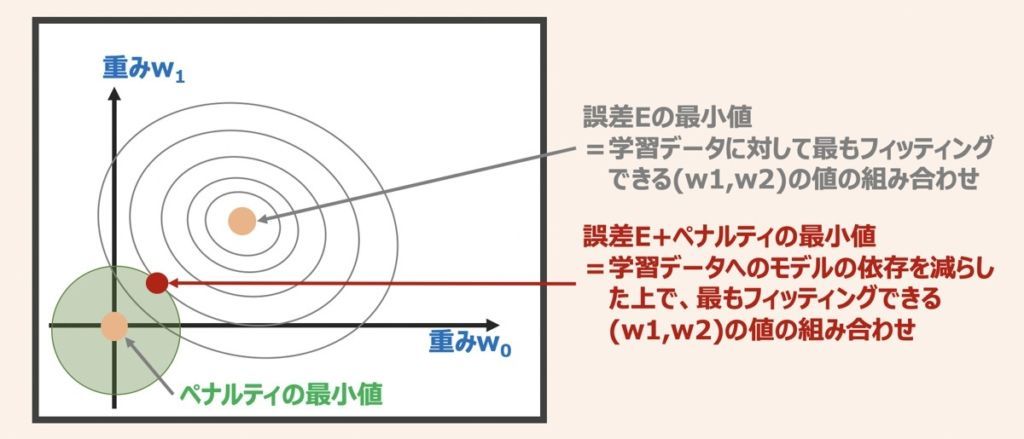
単純な例で重みw0とw1から取得できる誤差Eについて考えます。正則化を検討しない場合は誤差Eが最小となるように重みw0とw1の値を探索しますが、正則化を検討する場合はペナルティ項が導入されるため、重みの探索イメージは上図のような位置座標（赤プロット）をとるようなイメージとなります。

正則化の具体的な内容については下記の記事で紹介しています。

内部共変量シフトとBatch Normalization

ニューラルネットワークが多層化して複雑になると「学習が進みづらい、不安定化する」という問題が浮上します。原因の一つに、学習過程で更新される重みがあります。

ニューラルネットワークでは層の重みが更新されると、自動的にその層の出力も変化します。そして出力側に位置する次の層の入力値は前の層の出力であるため、その入力値も変化するのです。つまり、出力層側に近い層の入力値は、学習中常に変化し続けるような状態になってしまいます。その結果、日々変化する入力値に惑わされて重みの最適化が表面上一時停止した状態に陥ってしまうわけです。この現象を内部共変量シフトと言います。

Batch Normalizationは内部共変量シフトを回避し、多層のニューラルネットワークでも安定した学習を続けさせるための手法です。多層のニューラルネットワークを実装する際は考慮しましょう。