こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！
ニューラルネットワークにおける処理の流れ
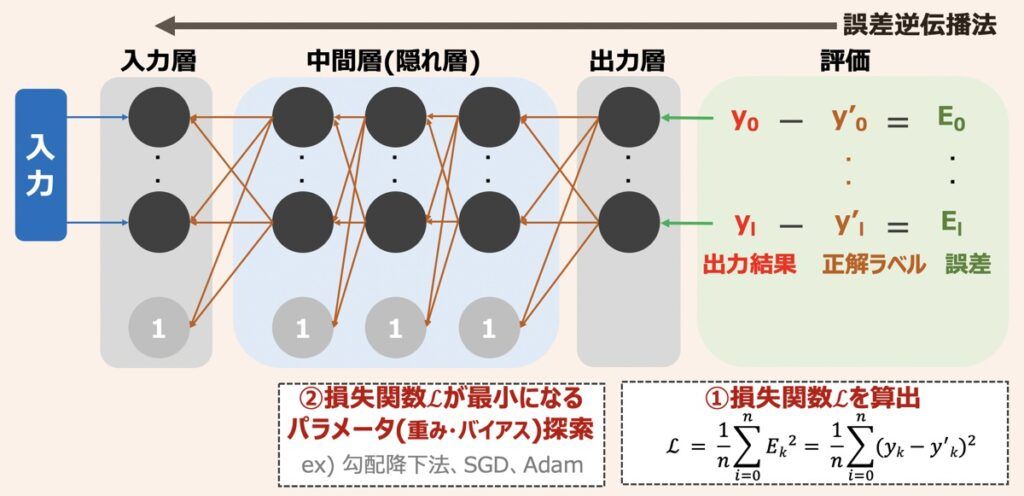
はじめに、ニューラルネットワークの学習の仕組みを概念図を解説します。
ニューラルネットワークの学習では、まず出力層から得られた出力結果が正解ラベルと比較され、出力結果と正解ラベルの差である誤差を算出します。続いて、各出力結果から得られた誤差の総和(損失関数)を求めます。ニューラルネットワークではこの損失関数を最小化することが学習と位置付けられています。求められた損失関数の値をもとにパラメーター(重みやバイアス等)を更新していき、損失関数小さくしていきます。最後に損失関数が最小となる際のパラメータ値を探索できた時点で学習完了となります。このような学習方法を「誤差逆伝播法」と言います。
本記事では「損失関数を最小化する仕組みとパラメータ探索アルゴリズムの役割」を詳細に解説します。カバーする範囲は下記です。
- 損失関数と勾配降下法
- 学習率
- 局所最適解と大域最適解
- 損失関数を最小化するためのパラメータ探索アルゴリズム
ここでニューラルネットワーク・ディープラーニング全体的な仕組みがどうなっているのか詳しく知りたい方は下記の記事をご覧下さい。
【深層学習】ニューラルネットワークの仕組みとディープラーニングモデル性能最適化のポイント解説
ディープラーニングの実装を検討している方向けです。深層学習モデルを実装するための仕組みとモデルを最適化する手法など重要なポイントを踏襲しています。本記事読了後、モデル改善に向けた適切なアプローチができるようになるでしょう。
損失関数と勾配降下法
「ニューラルネットワークモデルを最適化する」とは、出力結果と正解ラベルの誤差の総和である「損失関数」を最小化できるようなパラメータ(重みやバイアス等)を探し出すことを意味します。
損失関数の値はモデルの出力がどれだけ正解とずれているかを表す指標であり、下記の数式で示されます。
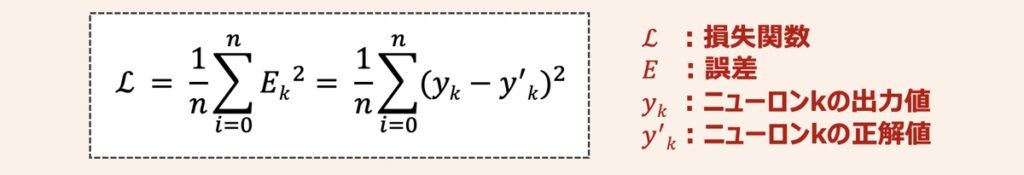
損失関数とパラメーター(重みやバイアス等)という軸でグラフを描いた場合、パラメータ数に応じて下記のように表せます。
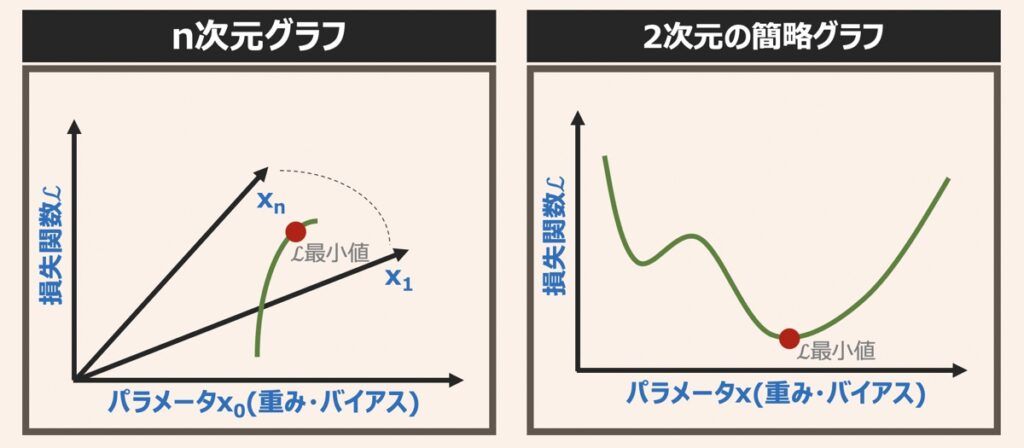
ニューラルネットワーク実装する上で、損失関数とパラメータの関係は、n次元で示される関係（上図左）のようになります。今回は理論主体の説明とするために、簡略化した上図右の2次元グラフを用いて話を進めます。
それでは本題です。損失関数の最小値はどうやって見つけ出すのでしょうか？
早速仕組みを見ていきましょう！
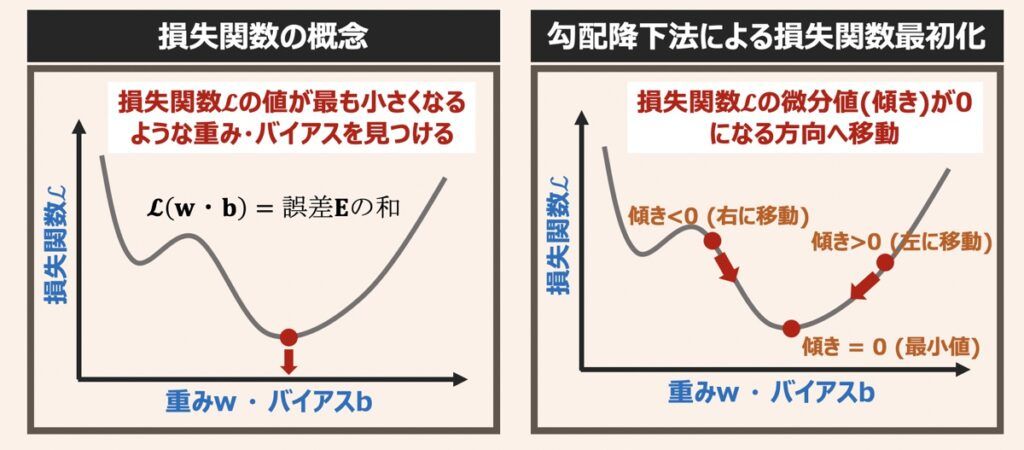
上図に損失関数を最小化するパラメータ探索プロセスを示します。
ここでポイントはニューラルネットワークモデルを最適化する学習初期(図左)では、グラフの全容が分からない（不明）ということです。つまり、「誤差出力→パラメータ更新」という地道な作業を繰り返していき、損失関数の値が最小となる点を探索していく必要があるわけです。
しかしながら、この探索方法だとあまりにも効率が悪く、計算コストが増大します。そこで損失関数の最小値を求める際は、パラメータ、損失関数の値に加えて「損失関数の傾き(勾配)」を用いるよう工夫するのです。傾きが0に近づく方向へ微小移動しながらモデルのパラメータを更新していくことで、損失関数が最小となるパラメータを効率的に見つけ出すことができます。
このように、損失関数の傾き(勾配)を算出し、傾き0=最小値と捉え、傾きが0となる方向へ移動するアルゴリズムを勾配降下法と言います。損失関数を最小化するためのパラメーター探索アルゴリズムとして一番シンプルかつ一般的なものです。
まとめ｜損失関数と勾配降下法
ここまで損失関数を最小化するパラメータ探索アルゴリズムの仕組みについて言及しました。後述では勾配降下法のようなパラメータ探索アルゴリズムの数学的理論について解説していきます。
学習率
損失関数が最小となるパラメータ(重み、バイアス等)を探索するアルゴリズムとして勾配降下法を言及しました。ここでは勾配降下法の数式を理解していきましょう。
上記数式を見ると新しい概念として、学習率(学習係数)が含まれていますね。
学習率とは、どれだけの大きさでパラメータxを移動させるかの割合を表しています。
イメージとして下記グラフを見てみましょう。
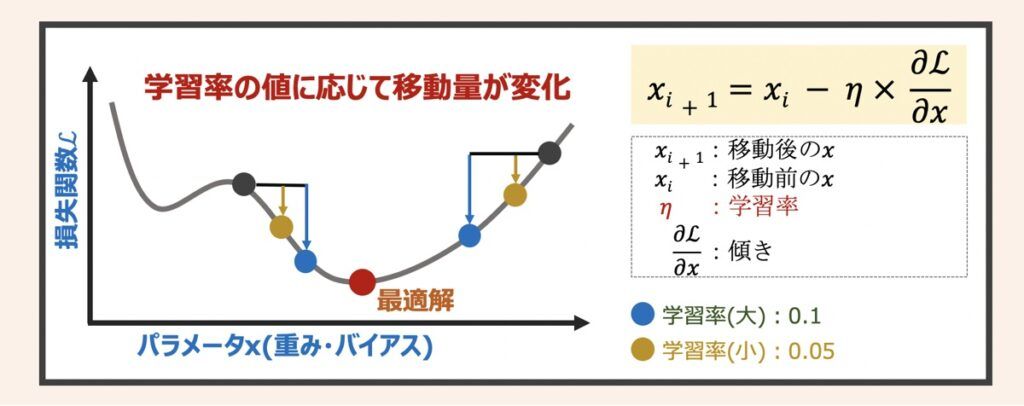
学習率の違いよるパラメータの移動イメージは上図になります。この学習率の設定はニューラルネットワーク最適化問題を解く上で非常に重要です。学習率の大小の違いが、パラメータ探索に与える影響を下記に示します(下記表の文言として、損失関数の最小値は最適解と言い換えています)。
| 学習率 | 利点 | 欠点 |
|---|---|---|
| 大きい | 移動量が大きいため、少ない計算量で早く最適解に到達する可能性が高い | パラメータxが最適解付近で発散して最適解に辿り着けない可能性がある |
| 小さい | 移動量が小さいため、精度の高い最適解を得る可能性が高い | 計算量が大きくなる。 局所問題に陥る可能性あり(詳細は後述) |
ニューラルネットワークを実装する際は、分析者自身が学習率を設定します。ハイパーパラメータによる自動探索を用いて最適な学習率を推定し、その値を設定することが多いです。
局所解問題(局所最適解と大域最適解)
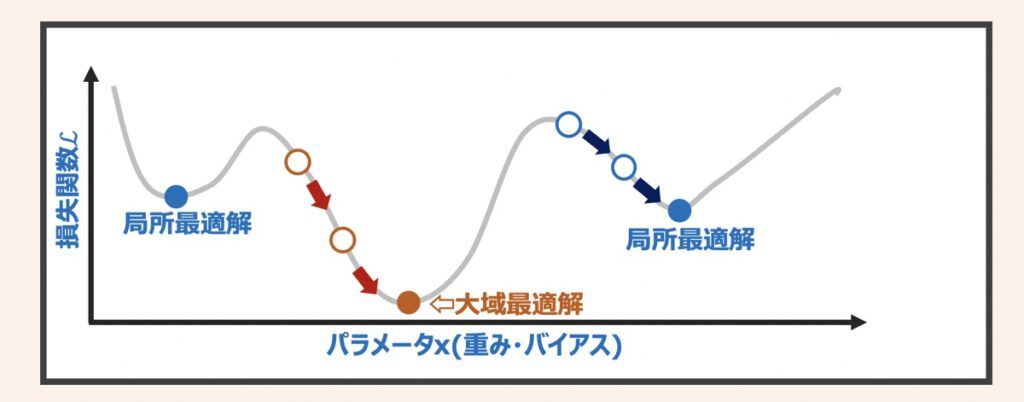
勾配降下法を利用することで全体的な関数の形が分からなくても、最小値が求められそうなことが分かりました。しかし、全ての状況で必ず損失関数の最小値に辿り着けるかというと、そう簡単ではありません。例として上図に示すような複数の山や谷がある関数を考えてみます。
損失関数が上図の形状をしていた場合、勾配降下法で計算を開始するスタート地点によっては最小値(大域最適解)にたどり着けないリスクがあります。例えば、○から計算を開始した場合、大域最適解に辿り着ける可能性が高くなります。一方で○から計算を開始した場合、局所最適解を最小値を見なしてしまう可能性が高くなります。これは勾配降下法が損失関数の傾き0=最小値と捉え、傾きが0となる方向にパラメータを更新するアルゴリズムだったため、このような現象が起こりうるのです。
局所最適解に収束しないようにする方法の１つに、前述した「学習率の大きさ」があります。学習率が大きいと、局所最適解の谷を超えて大域最適解に辿り着く可能性が高くなります。一方で学習率が高すぎると大域最適解付近に移動しても、大域最適解に収束できない可能性も高くなります。ニューラルネットワーク最適化の観点では、大域最適解に必ず収束するのは非現実的です。そのため、損失関数が小さければその点のパラメータ値で妥協し、モデル作成するのが現実的になっています。
損失関数を最小化するパラメータ探索アルゴリズムの種類と特徴
局所解問題を解決する手段の1つは「学習率を変化させること」と前述しました。
その他の解決手段として「パラメータ探索アルゴリズム(Optimizer)自体を変更すること」があります。勾配降下法を改良したアルゴリズムがいくつか提唱されており、以下それぞれの特徴をご紹介します。
確率的勾配降下法(SGD)
- 勾配計算で確率分布を加味した手法。
- 学習データの順番を入れ替えつつランダムに勾配降下法を適用することで、局所最適解に収束しづらくなる。
- 局所最適解を複数有する複雑な関数には適用が難しい。
Momentum SGD
- 確率的勾配降下法(SGD)に慣性の概念付与したアルゴリズム。
- 勾配を降りる方向に対して移動量が大きくなる。そのため早く収束する可能性が高くなる。
RMSprop
- 過去に計算した勾配の総和に基づき学習率を自動で調整できるアルゴリズム。
- 厳密には勾配の総和を指数移動平均で計算しており、直近の勾配情報を加味して学習率が調整される。
- Adagradという最適化アルゴリズムの改良版と言われている。
Adagrad
- 計算し終えた勾配の合計をもとに、パラメータ毎の学習率を調整できるアルゴリズム。
- 小刻みに探索したいパラメータは学習率を小さくし、広い間隔で探索したいパラメータは学習率を大きくなるように調整できる。
- 上記のようなパラメータ毎の学習率調整によって効率的なパラメータ探索処理を実現。
Adam
- AdagradやRMSpropとMomentum SGDを改良したようなアルゴリズム。
- 近年のパラメータ探索アルゴリズムの中で最も評価が高い。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に
お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら
