【Python×Keras】多層パーセプトロンとニューラルネットワークを作成する方法｜AI・機械学習入門

2022年6月11日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

本記事はニューラルネットワークによるPython実装イメージを深めるために作成しております。本記事を通じて「単純パーセプトロン」「多層パーセプトロン」「Kerasを用いた2層ニューラルネットワーク」の構築方法を学習しましょう。

【機械学習・AI】Pythonでのパーセプトロン構築方法

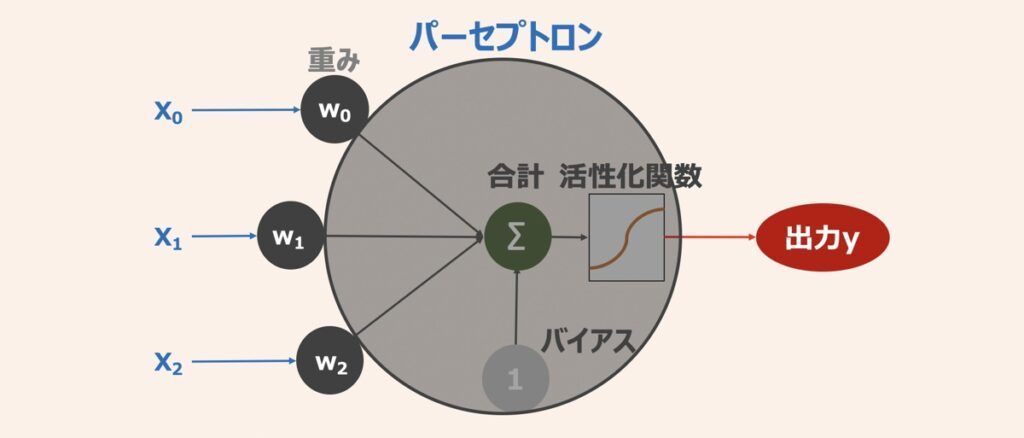
上記のような入力が3次元の単純パーセプトロンをPythonで実装します。下記のようにコーディングしてみましょう。

import numpy as np
import math

#パーセプトロン
  #3次元の入力
  #1次元の出力

def perceptron(Xn):
    
    # ①重み
    Wn = np.array([-0.8,1.2,0.6])
    
    # ②バイアス
    B = 0.25
    
    # ③入力値の重み付け(ベクトルの内積で計算) + バイアス
    XnWn = np.dot(Xn,Wn) + B
    
    # ④活性化関数で出力(シグモイド関数)を用いて出力
    Output = 1 / (1 + math.exp(-XnWn))
    
    return Output

#入力
Xn = np.array([0.2,0.3,-0.1])
#出力
print(perceptron(x))


# 出力結果
# 0.5962826992967878

①重みと②バイアスは任意に設定しています。③入力値の重み付けはnumpyのdot()メソッドで内積計算しています。④活性化関数は今回シグモイド関数を用いました。

パーセプトロンは上記①〜④の組み合わせで成り立っています。上記の記述方法はパーセプトロンの実装概念理解には役立ちますが、今後多層パーセプトロンやニューラルネットワークのように層を多層化していく場合、上記の書き方では効率が悪くなり管理が大変です。そのため後述ではKerasを用いて実装していくことにします。

Kerasを活用する場合、事前にライブラリのインストールが必要です。ターミナル・コマンドプロンプト等を開き、以下を実行しておきましょう。

pip install keras

【Keras×Python】多層パーセプトロンの構築方法

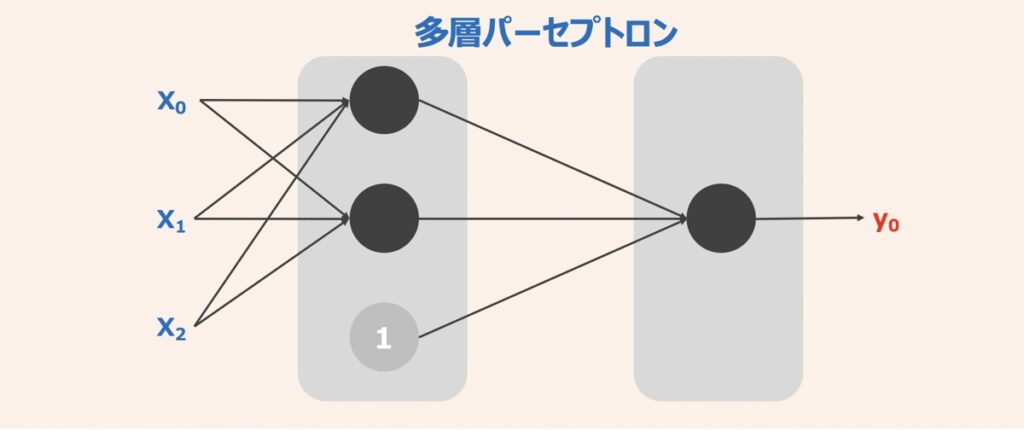
上記のような入力3次元・出力1次元の多層パーセプトロンをKerasを用いて実装します。以下のようにコードを記述してみましょう。

import numpy as np
from keras.layers import Dense
from keras.models import Sequential


#①入力を定義
 # ３次元の入力
 # 正解ラベルは0か1
X = np.array([
               [0.3, 0.2, -1.1],
               [0.2, 0.6, -0.9],
               [0.4, 0.3, -0.3],
            ])

y = np.array([0,1,0])

#②インスタンス
model = Sequential()

#③中間層作成
 # input_dim(入力の次元):3次元
 # units(パーセプトロン数):2つ
 # activation(活性化関数0: ReLU関数

model.add(Dense(units=2,activation="relu",input_dim=3))


#④出力層追加
 # input_dim(入力の次元):省略(前の層のperceptron数が2つなので自動的に2二次元に決定する)
 # units(パーセプトロン数):1つ
 # activation(活性化関数0: ReLU関数)
 # 出力は1次元

model.add(Dense(units=1,activation="relu"))


#⑤学習方法決定
 # loss(損失関数): binary_crossentropy(2分類問題で利用)
 # 損失関数を最小化するためのパラメータ最適化アルゴリズム(optimizer)：adam

model.compile(loss="binary_crossentropy",optimizer="adam")

#⑥学習
history = model.fit(X,y, epochs=1000)

まずKeras.model.Sequentialクラスをもとにモデルのインスタンスを作成します。

続いてそのインスタンスにKeras.layer.Denseメソッドで層を追加します。層は引数を用いることで詳細な定義が可能です。最後にcompile()メソッドで損失関数およびパラメータ最適化アルゴリズムを設定することでモデル定義完了です。あとはfit()メソッドを用いてモデル学習を行なってみましょう。

各層の重みとバイアスを確認する

作成したモデルにおける各層の重みとバイアスは、下記のようにlayersメソッドで層を指定し、get_weights()メソッドを適用することで確認できます。

# 層を指定し、重みとバイアスの値を確認
# 重み
print(model.layers[0].get_weights()[0])
# バイアス
print(model.layers[0].get_weights()[1])


# 出力結果：1層目重み
# [[-0.68150294  0.87695265]
#  [ 1.5706831  -0.8103228 ]
#  [-0.11128107  0.57601845]]
# 出力結果：1層目バイアス
# [-0.14229241  0.        ]

損失関数の誤差の変化を確認する

構築したモデルの評価では縦軸に損失関数、横軸にエポック数が一般に用いられます。今回簡単ではありますが下記のコードを実行し、エポック数における誤差の推移を確認してみましょう。

import matplotlib.pyplot as plt
%matplotlib inline
#フォントの日本語対応
from matplotlib import rcParams
rcParams["font.family"] = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"

loss = history.history['loss']  

plt.plot(np.arange(len(loss)), loss, label="訓練用データの誤差")
plt.legend()
plt.show()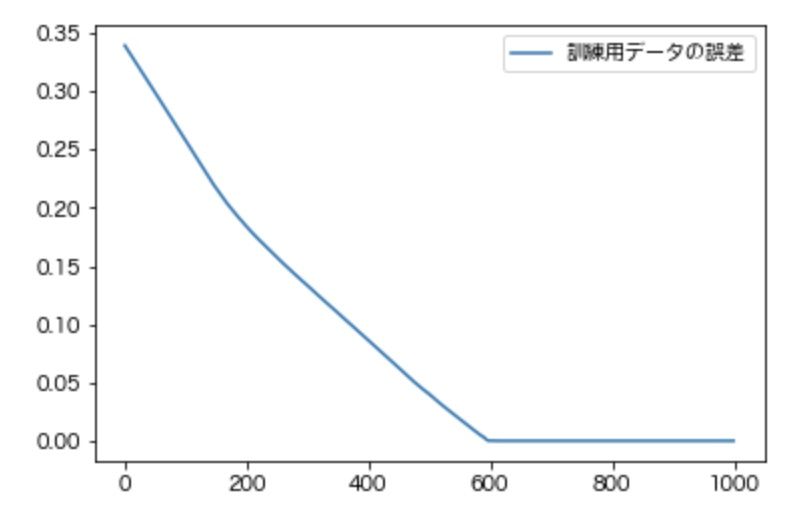

【Keras×Python】ニューラルネットワークの実装方法

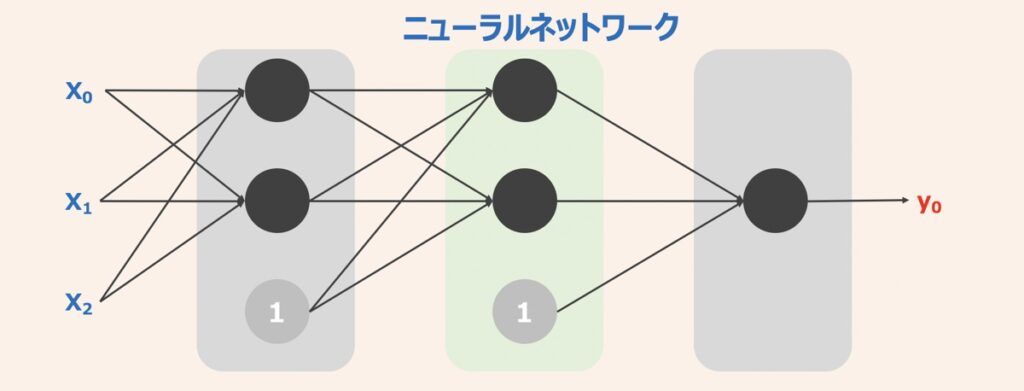
最後に上記のようなニューラルネットワークをKerasを用いて作成してみましょう。手順は上述の多層パーセプトロンと同様です。以下コードを確認してみましょう。

import numpy as np
from keras.layers     import Dense
from keras.models     import Sequential
from keras.optimizers import Adam


#①入力を定義
 # ３次元の入力
 # 正解ラベルは0か1
X = np.array([
               [0.3, 0.2, -1.1],
               [0.2, 0.6, -0.9],
               [0.4, 0.3, -0.3],
            ])

y = np.array([0,1,0])

#②インスタンス
model = Sequential()

#③1層目
 # input_dim(入力の次元):3次元
 # units(パーセプトロン数):2つ
 # activation(活性化関数0: ReLU関数

model.add(Dense(units=2,activation="relu",input_dim=3))

#④2層目
 # input_dim(入力の次元):省略(前の層のperceptron数が2つなので自動的に2二次元に決定する)
 # units(パーセプトロン数):2つ
 # activation(活性化関数0: ReLU関数
    
model.add(Dense(units=2,activation="relu",input_dim=3))

#④出力層
 # input_dim(入力の次元):省略(前の層のperceptron数が2つなので自動的に2二次元に決定する)
 # units(パーセプトロン数):1つ
 # activation(活性化関数0: sigmoid関数

model.add(Dense(units=1,activation="sigmoid"))


#⑤学習方法決定
 # loss(損失関数): binary_crossentropy(2分類問題で利用)
 # 損失関数を最小化するためのパラメータ最適化アルゴリズム(optimizer)：adam
 # 学習率(lr):0.01

model.compile(loss="binary_crossentropy",optimizer=Adam(lr=0.01))

#⑥学習
history = model.fit(X,y, epochs=1000)