こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- 回帰分析とは・導出・評価方法を知りたい
- 単回帰モデルと重回帰モデルの違いを理解したい
- 回帰モデル作成時の評価方法やモデル性能改善方法を知りたい
回帰分析とは
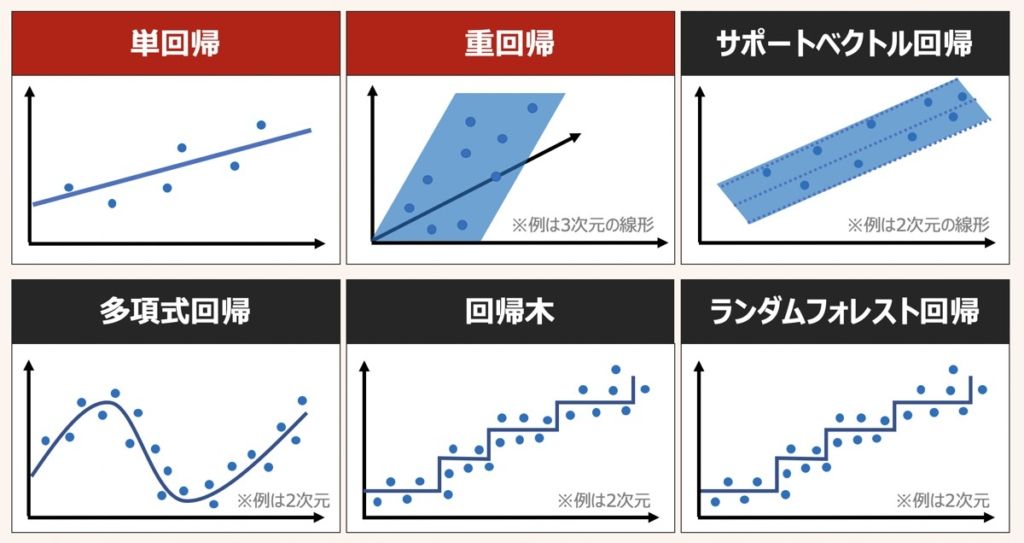
回帰分析とは、(カテゴリ値や離散値ではなく)連続値に基づき、ある結果を予測する分析手法を指します。
回帰モデルとは、回帰分析をもとに、1つ以上の独立変数(説明変数)と連続値の従属変数(目的変数)との関係を表現したものを指します。
機械学習の世界において、回帰モデルは教師あり学習の1つに位置付けられます。
線形回帰と非線形回帰モデル
線形回帰モデル(Linear Regression)とは、説明変数と目的変数の関係を直線的な関数(線形関数)として表現できるモデルを指します。
一方で、非線形回帰モデルは、変数間の関係性が直線的ではなく、多項式関数を用いて表されます。
本記事では線形をベースとした単回帰・重回帰分析について詳しく解説します。
単回帰分析とは
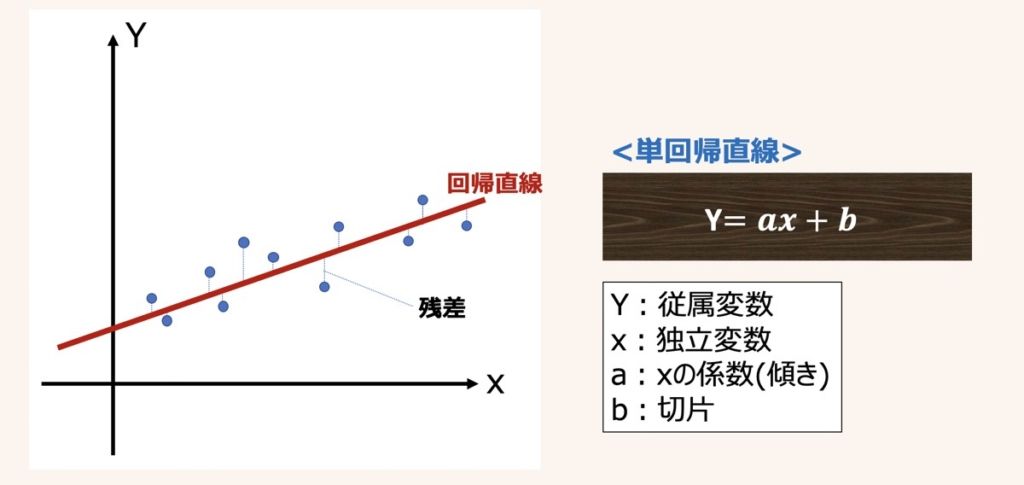
単回帰分析とは、単一の独立変数(説明変数)xに基づいて,連続値をとる従属変数(目的変数)Yを予測する分析手法です。説明変数が1つだけの単回帰モデルの方程式は上図のように示されます。
実測値に基づくサンプル(xn, yn)に適合するように引かれた直線を回帰直線と呼びます。
得られた回帰直線(方程式)をもとに未知の値Yを予測するには、既知の説明変数xを方程式に代入することで、予測値が得られます。
回帰直線から各サンプルへ伸びる縦線は残差(予測誤差)と呼ばれ、実測値と予測値の誤差を示しています。
最小二乗法による単回帰式の導出
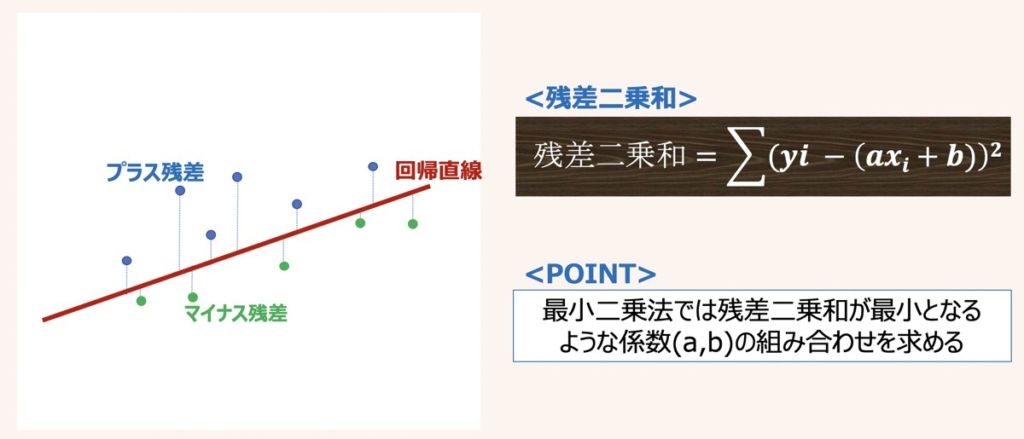
ある目的変数Yを正確に予測するための単回帰式を導出するための重要ステップとして、最適な係数aとbの推定があります。
係数a,bを決めるには最小二乗法という方法が一般的に用いられます。
最小二乗法とは、サンプルの実測値と回帰式から得られる残差の二乗和を計算し、残差二乗和が最小となる(a,b)を推定する手法を指します。
最小二乗法により残差二乗和が最小となる(a,b)を推定した後は、単回帰式y=ax+bとして係数を当てはめると導出完了です。
重回帰分析とは
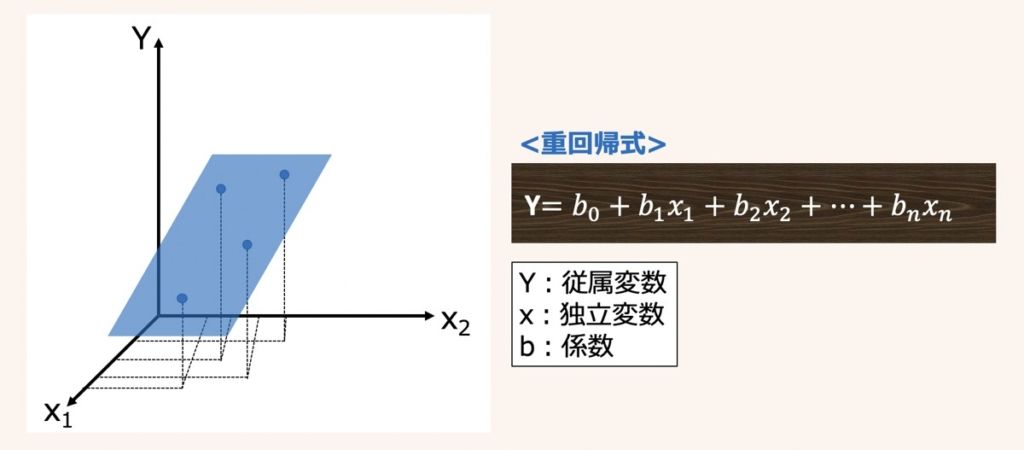
重回帰分析とは、複数の独立変数(説明変数)x1~xnに基づいて,連続値をとる従属変数(目的変数)Yを予測する分析手法です。
上図に3次元の重回帰グラフの例(左図)とn次元の重回帰式(右図)をそれぞれ示します。
重回帰式のb0は目的変数Yの切片、b1〜bnは説明変数x1〜xnの係数を表しています。
単回帰と重回帰分析の違い
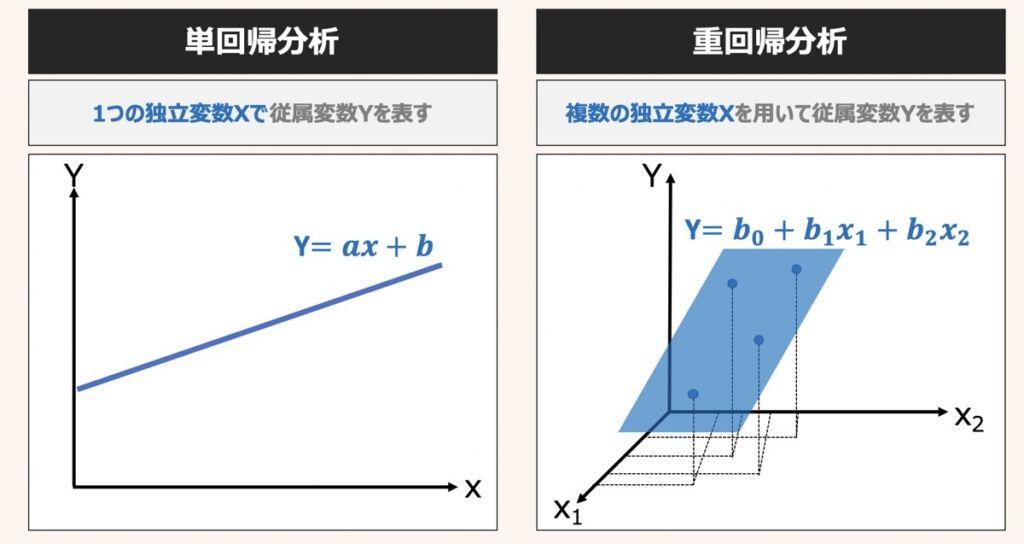
単回帰と重回帰の違いは、Yの予測に用いる説明変数xの数にあります。
重回帰式は説明変数xを複数用いてYを予測するのが特徴です。
最小二乗法による重回帰式の導出
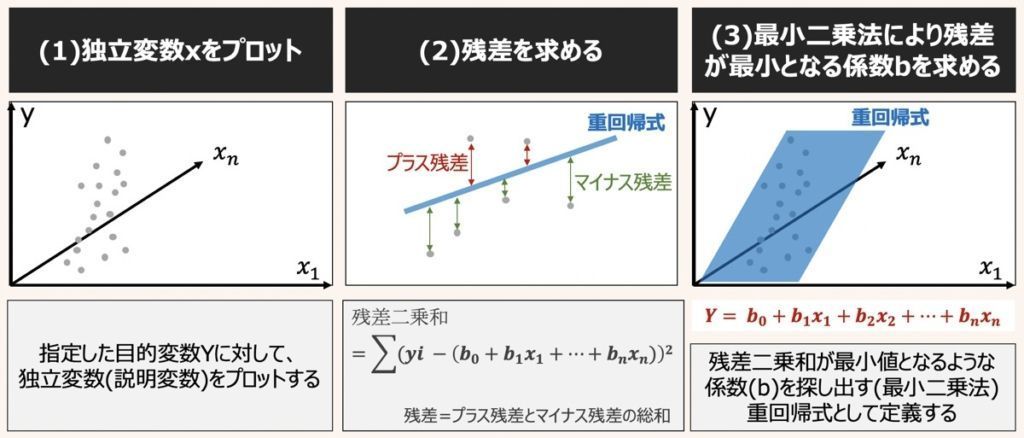
重回帰の方程式においても単回帰同様、最小二乗法を用いて導出します。
重回帰分析における最小二乗法の適用では、サンプル点と重回帰式に対する残差二乗和(SSE)を最小化する係数b0〜bnを推定することが目的です。
ここで最小二乗法の指標として用いる縦の距離(残差または誤差)には、具体的にRMSEまたはMAEが用いられます。
RMSE(平均平方二乗誤差)

RMSE(Root Mean Square Error)は「予測誤差の二乗平均を集計した指標」で、値が小さいほど回帰モデルの性能が高いことを意味します。
MAE(平均絶対誤差)

MAE(Mean Absolute Error)は「予測誤差の絶対値を平均して算出する指標」で、RMSE同様、値が小さいほど回帰モデルの性能が高いことを意味します。
MAEはRMSEと比較して外れ値に強いため、データセットに外れ値が多く含まれる場合によく用いられます。
回帰モデルの評価方法
回帰モデルの評価意義として以下2つがあります。それぞれ見ていきましょう!
- 回帰モデルの予測性能評価
- 回帰モデルの検定(統計的有意性評価)
回帰モデルの予測性能評価
回帰モデルの予測性能を評価する代表的指標には、前述したRMSE・MAEや決定係数(R2)があります。
機械学習・統計解析で回帰モデルを取り扱う方向けに、下記の記事で回帰モデルの評価指標の解説を行っています。本記事と合わせてご覧下さい。
【AI・機械学習】回帰モデルの性能評価および評価指標の解説|決定係数・RMSE・MAE・残差プロット
機械学習の性能評価方法の中で「回帰モデルはどうやって評価するの?」本記事ではその疑問に回答します。具体的に、決定係数、RMSE、MAE等の評価指標があり、それら特徴・利用シーンを1つずつ詳しく解説します。
回帰モデルの統計的有用性評価
特に重回帰モデルにおいて、統計的有用性を評価するために、分散分析および回帰係数のt検定が適用されます。
分散分析
分散分析とは、いくつか分けれらたグループの平均が全て等しいという帰無仮説を立て、分散比(F値)を検定統計量とし、F分布を検定する手法です。
帰無仮説と対立仮説は下記のように立て、重回帰モデルの有意性を評価します。
- 帰無仮説:回帰モデルの説明性が0(有意性なし)
- 対立仮説:回帰モデルの説明性あり(有意性あり)
設定した帰無仮説をもとに、回帰と誤差の2つの自由度からF値を計算し、設定した有意水準とF分布と照らし合わせ、p値を評価します。
有意水準は一般的に0.05と設定されることが多いです。p値が0.05以下であれば帰無仮説が棄却され、「回帰モデルの有意性あり」という対立仮説が採択されます。これは、目的変数の変動が統計的検定によっても確認できたことを指します。
回帰係数のt検定
回帰係数とは、回帰分析で得られる回帰方程式の各説明変数の係数(傾きや切片)です。t検定とは、帰無仮説が正しいと仮定した際、統計量がt分布に従うことを利用した統計学的検定手法の総称を指します。
帰無仮説と対立仮説を下記のように立て、重回帰モデルの有意性を評価します。
- 帰無仮説:回帰係数の説明性が0(有意性なし)
- 対立仮説:回帰係数の説明性あり(有意性あり)
検定統計量のt値は回帰係数/標準誤差として算出できます。そして、t分布からp値を計算し、有意水準と照らし合わせます。
p値が有意水準より小さい場合、帰無仮説は棄却され、「回帰係数の説明性あり」という対立仮説が採択されます。これは、説明変数の目的変数に対する説明力が統計的にも確認できたことを意味します。
回帰モデルにおける予測性能を改善するためのデータ準備
回帰モデルの予測性能の改善手段として、回帰モデル導出の元となったデータサンプルに焦点を当てた性能改善手法をいくつか解説します。
極端な外れ値を除去する
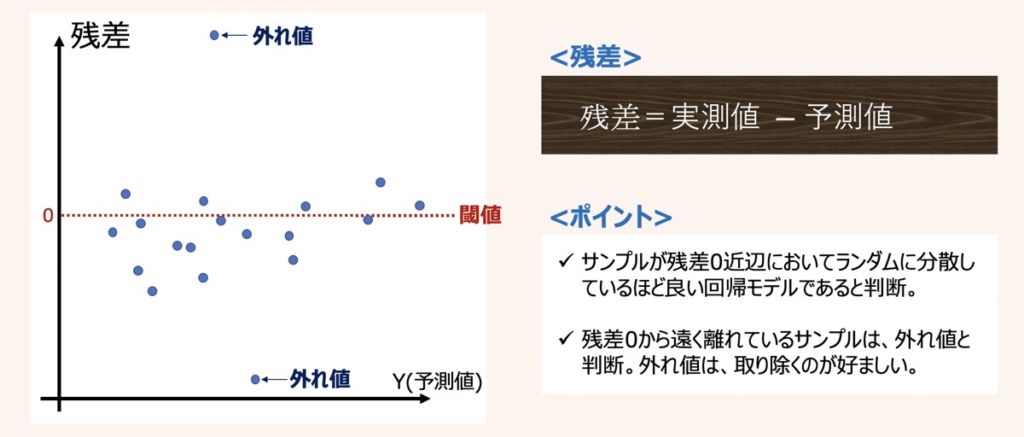
データサンプルに極端な外れ値が含まれる場合、回帰モデルは外れ値情報に引っ張られてしまうため、予測性能に悪影響を及ぼす結果につながってしまいます。そのため、極端な外れ値はサンプル群から取り除くのが良いでしょう。
極端な外れ値は、上図のような回帰診断図を用いて可視化することで区別できます。
回帰診断図の代表的なものとして残差プロットがあります。その他正規QQプロットや残差平方根プロット等も外れ値確認のためによく用いられます。
自己相関の検証
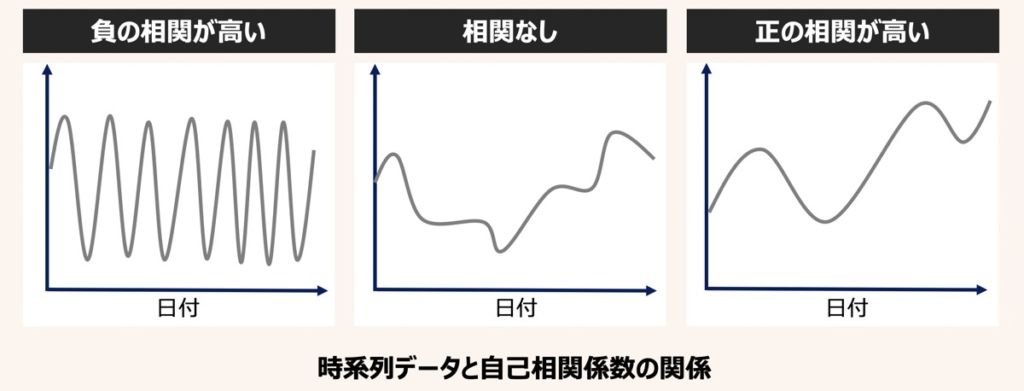
自己相関とは、ある日付断面の変数Aと時系列をずらした同一変数A’間の相関を指します。
例えば、連続したX-1、Xという変数があるとします。現在の値(X)は直前過去の値(X-1)とどれほど相関があるのか確認したい場合に自己相関係数を算出するのです。
特に重回帰モデルに対して、時系列データを説明変数として用いる場合、その説明変数の自己相関係数は、無相関(ゼロに極めて近い)を示す必要があります。
自己相関が強い説明変数を入れると、回帰モデルの実態より高い決定係数を出力してしまうためです。機械学習の世界に例えると、汎化性能が劣化した過学習のイメージに近しいでしょう。
重回帰モデルに適用する説明変数は、あらかじめ自己相関係数を確認し、自己相関が強い変数は除外することによって、モデル性能改善につながるでしょう。
多重共線性がないことを確認
多重共線性があるとは、重回帰モデルに用いる説明変数同士で強い相関があることを指します。
多重共線性がある変数を用いることは、あたかも同じ複数の変数をモデルに取り入れたことを意味します。同じ変数を複数用いても回帰モデルの性能向上に役立つことはなく、編回帰係数の信頼性が無くなってしまうため、むしろ数値的に不安定な予測を引き起こしてしまいます。
そのため、重回帰モデルを作成する際は、説明変数間同士に多重共線性がないか必ず確認が必要です。
多重共線性の確認手段と回避方法
n次元の特徴量(X1,X2,・・・Xn)がある中で、Xiを目的変数、Xi以外を説明変数と置き、Xiを回帰分析した時の決定係数Ri2を求めたとします。決定係数は1に近いと、目的変数(Xi)が説明変数(Xi以外)でほぼ説明できてしまっていると言えます。
つまり、決定係数が1に近い時は多重共線性があると判断し、目的変数に置いたXiを取り除くのが良いです。
決定係数を用いて実際に多重共線性を判断する指標として、トレランス(tolerance, 許容度)とVIF(Variance Inflation Factor,分散拡大要因)を用います。

VIFiが10以上を示した場合、多重共線性があると判断し、対象の変数Xiを取り除くのが良いされています。また、VIFが5以下であれば、多重共線性がない望ましい値とされています。
Pythonプログラミングによる回帰モデルの作成・評価方法
Pythonを用いて実際に単回帰・重回帰モデルを構築する方法は、下記の記事で解説しています。
【機械学習・Python】線形単回帰・重回帰分析に基づき予測モデルを作成|scikit-learnでモデル開発・評価
Pythonとscikit-learnを用いて単回帰および重回帰モデルを作成・評価する方法について解説します。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




