【機械学習×Python】HyperOptによるハイパーパラメータ最適化とロジスティック回帰モデル構築

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

【機械学習】ハイパーパラメータとは

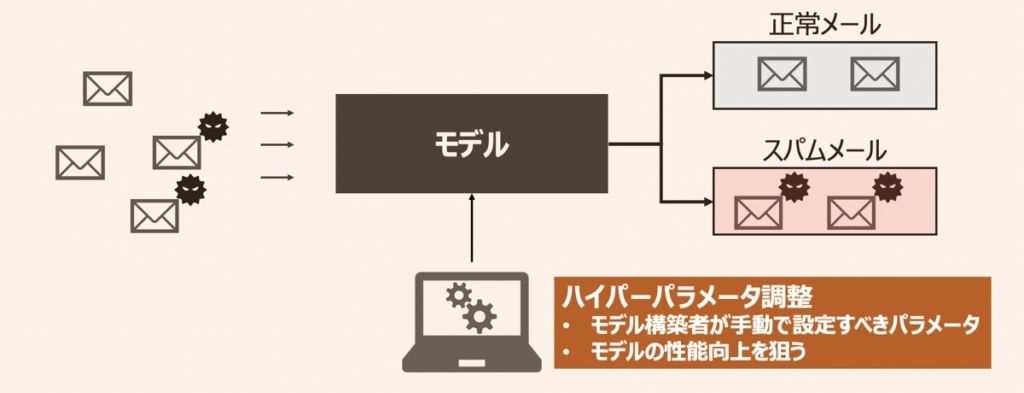
機械学習モデルを活用したアプリケーションには、設計者・モデル構築者が設定しなければならないパラメータが多数あります。それらパラメータを「ハイパーパラメータ」と呼び、主に機械学習モデルの予測・分類精度向上を目的に設定されます。ハイパーパラメータについて詳しく内容を知りたい方は、まずこちらの記事をご覧ください。

HyperOptとは｜ハイパーパラメータ探索メソッド

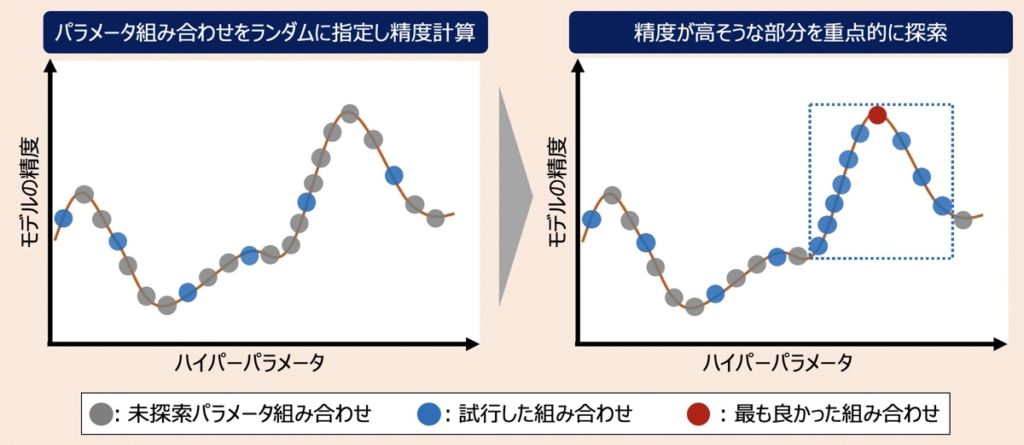
HyperOptとは、機械学習モデルで最適なパラメータ組み合わせを見つけ出すための探索手法です。ランダムサーチとSMBO(Sequential Model-Based Optimization)の一種として位置付けられています。

SMBOとは内部に計算の軽い近似モデルを保有するハイパーパラメータ探索手法であり、そのモデルをもとにパラメータを逐次更新しながら最適なパラメータ組み合わせを探索する手法を指します。

SMBOの処理では、最適なパラメータ組み合わせを判断するために、パラメータ組み合わせ毎に損失関数を適用し予測誤差を算出しています。ここで、損失関数には特定の計算ロジックを採用できるという特徴があり、その中でもTree-structured Parzen Estimator Approach（TPE）というロジックを採用しているものがHyperOptとして位置付けられています。

ロジスティック回帰とは

ロジスティック回帰分析とは、ある事象の発生確率Pを予測する統計学的手法になります。多変量解析や機械学習における教師あり学習の2値分類問題として取り扱われます。

ロジスティック回帰の理論はこちらの記事で詳しく解説しています。

本記事ではHyperOptというパラメータ探索アルゴリズムをロジスティック回帰モデルに適用し、最適なパラメータを探索する方法について解説していきます。なお、HyperOptはロジスティック回帰以外にも簡単に適用できます。本記事で基本的なプログラミング方法を習得し、他の機械学習モデルにも適用できるようになることを目指しましょう！

【Python】Hyperoptでパラメータ最適化・ロジスティック回帰モデルを構築

それでは実際にPythonコードを触りながらハイパーパラメーターチューニングとモデル構築を実施していきましょう！下記の手順で進めていきます。

1. Pythonライブラリのインストール
2. データセットの説明
3. データの準備
4. ロジスティック回帰モデルを適用した目的関数の作成
5. Hyperoptによるハイパーパラメータチューニング
6. 性能評価

Pythonライブラリのインストール

後述のプログラム実行に際して、次のようなPythonライブラリを活用します。事前にインストールしましょう。

ロジスティック回帰

pip install scikit-learn

Hyperopt

pip install hyperopt

データセットの説明

データセットには、機械学習のサンプルデータとして有名なIris（アヤメ）データセットを活用します。3種類のアヤメ(Iris Setosa, Iris Versicolor, Iris Virginica)があり、それぞれ50サンプルずつ(合計150サンプル)用意されているデータです。このアヤメの名前を目的変数として利用します。また、説明変数にはアヤメの計測値である萼片（sepals）と花びら（petals）の長さと幅の4つを利用します。

データの準備

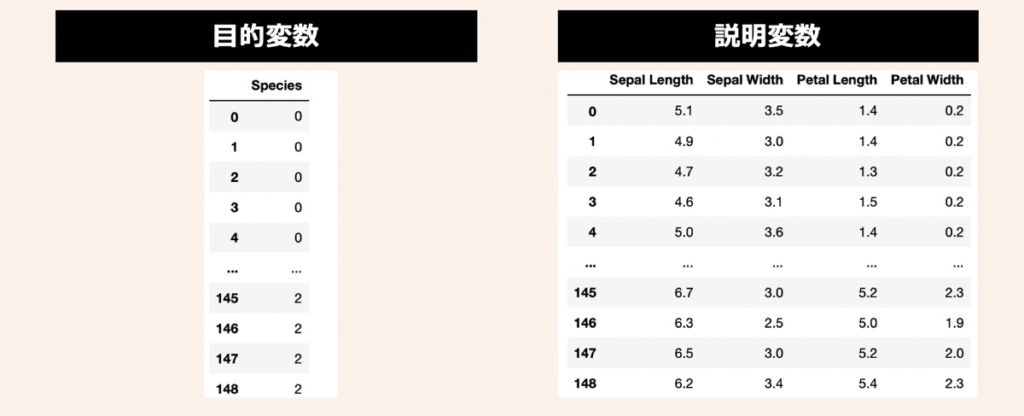
まず、前述したアヤメのデータセットを準備します。上記目的変数と説明変数をPandas形式で取り扱うために、下記のコードを実行してみましょう。

"""
=====================================================================
①データセットの準備(Sckit-learnで提供されているアヤメのデータを利用)
=====================================================================
"""
import numpy as np
import pandas as pd
from sklearn import datasets

# データロード
iris = datasets.load_iris()

# 説明変数
X = iris.data
X = pd.DataFrame(X, columns=["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"])

# 目的変数
Y = iris.target
Y = iris_target = pd.DataFrame(Y, columns = ["Species"])

後述では変数(X)を説明変数の集合体、変数(Y)を目的変数として利用していきます。今回データ加工やクレンジング、特徴量エンジニアリング等の前処理工程は割愛します。

ロジスティック回帰を適用した目的関数の作成

パラメータ値の組み合わせを受け取って値を返す関数を目的関数と呼びます。

次のような目的関数を記述しましょう。

"""
=====================================================================
②目的関数の作成（ロジスティック回帰）
=====================================================================
"""
from sklearn.linear_model    import LogisticRegression
from sklearn.metrics import accuracy_score

# 目的関数を作成
def objective(args):
    
    # ロジスティック回帰モデルインスタンス
    model = LogisticRegression(penalty=args["penalty"],   # 正則化項(L1正則化 or L2正則化等が選択可能)
                               C=float(args["C"]),        # 正則化の強さ
                               solver='liblinear',        # パラメータ探索アルゴリズム
                              )
    # モデル学習
    model.fit(X_train,Y_train)
    
    # 予測結果算出
    Y_pred   = model.predict(X_test)
    
    # 評価（正解率）
    accuracy = accuracy_score(Y_pred,Y_test)
    
    # Hyperoptは目的関数の最小化が目的であるため、accuracyの出力にはマイナスを付与
    return -accuracy

上記の目的関数では次のような処理を順番に実行しています。

1. 引数でハイパーパラメータの組み合わせを受け取る
2. パラメータの組み合わせをもとに機械学習モデル（今回はロジスティック回帰）を学習させる
3. 学習済みモデルをもとに予測誤差（今回は正解率を採用）を評価する
4. 予測誤差を返り値として渡す

この目的関数は、とりうるパラメータ組み合わせ数の分だけ実行されます。そして、目的関数の返り値が最小になるパラメータ組み合わせが見つかると、実行処理が終了するというものです。

今回予測誤差の評価には正解率accuracyを採用していますが、正解率以外の評価指標も設定可能です。分類問題の評価指標についてはこちらの記事で詳しく解説しています。

【モデル学習】Hyperoptによるハイパーパラメータチューニング

前述の目的関数に渡すパラメータ候補parametersおよび最適なパラメータ組み合わせbest_parametersを算出するために、以下のコードを実行しましょう。目的関数内での予測誤差を評価するために、学習データとテストデータの分割も併せて行います。

ハイパーパラメータ探索

"""
=====================================================================
③モデル学習
　・ロジスティック回帰を分類アルゴリズムとして利用
　・ハイパーパラメータのチューニング手法にはHyperoptを採用
 =====================================================================
"""

from hyperopt import fmin,hp,tpe
from sklearn.model_selection import train_test_split

# 学習データ＆テストデータ分割
X_train, X_test,  Y_train, Y_test = train_test_split(X.values,Y.values,test_size=0.3, random_state=3)


# ハイパーパラメータ候補
parameters = {
    "penalty":hp.choice("penalty",('l2','l1')), # hp.choice()：選択肢を事前に設けて探索（返り値はインデックスの値）
    "C":hp.quniform("C",0.1,1,0.1),             # hyperopt.hp.quniform()：最小値0.1、最大値1を0.1刻みの値をランダム探索  
             }


# HyperOptによるパラメータ探索
best_parameters = fmin(objective,          # 目的関数
                       parameters,         # パラメータ組み合わせ候補
                       algo=tpe.suggest,   # 探索アルゴリズム
                       max_evals=30,       # 試行回数の上限
                       )

Pythonライブラリでは、fmin()というHyperOptの基本関数が用意されています。「探索対象のパラメータ組み合わせ候補」と「パラメータ組み合わせを受け取って損失関数の残差（予測誤差）を出力する関数」を与えると、fmin()はその残差を最小化する最適なパラメータ組み合わせを効率的に探索してくれます。

出力結果を確認

得られた最適なパラメータ組み合わせbest_parametersを出力すると次のような結果が確認できます。ここで、前述のパラメータ候補parameters指定時にhp.choice()で選択した出力値はインデックスになることに注意が必要です。

今回の例ではpenalty: 0は’L2’を指します。

# 最適なパラメータ値を出力
print(best_parameters)

# 出力イメージ
# {'C': 0.8, 'penalty': 0}

【モデル再学習】最適なハイパーパラメータでロジスティック回帰モデル構築

HyperOptをもとに探索した最適なパラメータbest_parameters組み合わせを用いてロジスティック回帰モデルを再学習しましょう。

# ベストパラメータを活用してモデル再学習
model = LogisticRegression(penalty="l2",              # 正則化項(L1正則化 or L2正則化が選択可能)
                           C=best_parameters["C"],    # 正則化の強さ
                           solver='liblinear',        # パラメータ探索アルゴリズム
                          )
# モデル学習
model.fit(X_train,Y_train)

【参考】ロジスティック回帰で使用するパラメータ一覧

ロジスティック回帰モデル構築時に本記事では代表的なパラメータのみを活用しました。細かくパラメータを指定したい場合は以下の記事が参考になるかと思われます。

モデル性能評価

最後に今回構築したモデルの精度を見てみましょう！

正解率ベースで算出すると、約98%という結果が得られました。

# 予測結果算出
Y_pred   = model.predict(X_test)

# 評価（正答率）
accuracy = accuracy_score(Y_pred,Y_test)

# 結果出力
print(accuracy)

【参考】AI・機械学習における配信情報まとめ

当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。

【仕事探し】副業・転職・フリーランス

副業・転職・フリーランスのAI案件の探し方

AIエンジニアの方向けに副業・転職・フリーランスとして始められる「AI・機械学習案件の探し方」について解説

AI・機械学習案件の探し方Python副業案件の探し方

【教育】おすすめ勉強法

AI・機械学習のおすすめ勉強法

AI・機械学習およびPythonプログラミングの知見を深めたい方向けに、おすすめの「勉強教材」「プログラミングスクール」を紹介

学習教材を見る厳選のAIスクールを見る

【参考】記事一覧

AI・機械学習記事一覧

AI・機械学習理論の基礎から最新のPythonプログラミング手法に至る幅広い情報を配信中

記事一覧を見る

最後に