こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- Pythonでロジスティック回帰モデルを構築する方法が知りたい
- ロジスティック回帰モデルの評価方法が知りたい
ロジスティック回帰モデルとは

ロジスティック回帰分析とは、ある事象の発生確率Pを予測する統計学的手法になります。多変量解析や機械学習における教師あり学習の2値分類問題として取り扱われます。上記のように、説明変数を入力した際、ロジスティック関数をもとに発生確率Pを求め、最終的に0か1を返すモデルをロジスティック回帰モデルと呼びます。
ロジスティック回帰についてもっと詳しく知りたい方向けにこちらの記事も配信しています。
ロジスティック回帰分析とは|統計学・機械学習理論に基づき徹底解説!
ロジスティック回帰分析とは何か知りたい方向けに「ロジスティック回帰の概要」と「関数の導出方法」について詳しく解説します。
【Python×機械学習】scikit-learnでロジスティック回帰モデルを構築・評価
PythonのScikit-learnライブラリを用い、ロジスティック回帰モデルを構築する方法について解説します。
具体的に下記の手順でプログラムを構築していきます。
- データセットの説明
- データの準備
- データの加工
- 特徴量選択
- モデル学習
- モデルの学習結果確認
- モデル推論
- モデル性能評価
データセットの説明
利用するデータセットは、タイタニック号の乗客員データになります。
このデータセットはKaggle Titanic – Machine Learning from Disasterよりダウンロードできます。
タイタニックのデータセットには次のような変数が格納されています。
| 変数名 | 概要 | キー |
|---|---|---|
| survived | 生存有無 | 0 = No 1 = Yes |
| pclass | チケットクラス | 1 = 1st 2 = 2nd 3 = 3rd |
| sex | 性別 | |
| Age | 年齢 | |
| sibsp | 一緒に乗船した兄弟/配偶者の数 | |
| parch | 一緒に乗船した親/子どもの数 | |
| ticket | チケット番号 | |
| fare | 旅客運賃 | |
| cabin | キャビン番号 | |
| embarked | 乗船港 | C = Cherbourg Q = Queenstown S = Southampton |
機械学習モデルを用いて、難破船を生き延びた乗客(Servived=1)を予測するモデルを作成します。
データの準備
前述したタイタニック号のデータセット読込のために、次のようなコードを実行します。
コード
import numpy as np
import pandas as pd
from sklearn import datasets
# データセット(train.csvを利用)
df = pd.read_csv("titanic/train.csv")データ出力結果(df)
データ加工
モデルが学習しやすいように、あらかじめデータセットを加工することとします。
次のようなデータ加工を実行してみましょう。
データ加工|数値変換
次に示すような文字列の変数を数値変換します。
# 性別を[0,1]変換
def gender_convert(x):
if x == 'male':
return 0
elif x == 'female':
return 1
# 港を数値変換
def embarked_convert(x):
if x == 'C':
return 0
elif x == 'Q':
return 1
elif x == 'S':
return 2
# 性別を数値変換
df["Sex"] = df["Sex"].apply(gender_convert)
# 港を数値変換
df["Embarked"] = df["Embarked"].apply(embarked_convert)データ加工|特徴量スケーリング(標準化)
次に示すような変数の尺度を揃えるために、特徴量スケーリングを実施します。
from sklearn.preprocessing import StandardScaler
# 標準化インスタンス (平均=0, 標準偏差=1)
standard_sc = StandardScaler()
# 年齢と運賃を標準化
X = df.loc[:, ['Age','Fare']]
X = standard_sc.fit_transform(X)
#標準化後のデータ出力
df.loc[:, ['Age','Fare']] = X特徴量スケーリングについて具体的に知りたい方向けに次のような記事も配信しています。
【Python】正規化・標準化による特徴量スケーリング|機械学習におけるデータ前処理入門
機械学習のデータ前処理で実施される「特徴量スケーリング(Feature Scaling)って何?」「重要性とは?」「どうやってスケーリングするの?」本記事ではこれらの質問に回答します。特徴量スケーリングとして代表的な正規化および標準化や、sckit-learnを用いたPythonプログラミング手法も解説しています。
データ加工|欠損値の除去
今回の例では欠損値を含むデータを行毎削除することとします。
# 各種特徴量における欠損値数の確認
df.isnull().sum()
# 出力イメージ
# PassengerId 0
# Survived 0
# Pclass 0
# Name 0
# Sex 0
# Age 177
# SibSp 0
# Parch 0
# Ticket 0
# Fare 0
# Cabin 687
# Embarked 2
# dtype: int64# 欠損値がある行を除去
df = df.dropna(axis=0).reset_index(drop=True)
# 欠損値がある行が除去されたことを再確認
df.isnull().sum()
# 出力イメージ
# PassengerId 0
# Survived 0
# Pclass 0
# Name 0
# Sex 0
# Age 0
# SibSp 0
# Parch 0
# Ticket 0
# Fare 0
# Cabin 0
# Embarked 0
# dtype: int64欠損値の取り扱いについて詳しく知りたい方向けに次のような記事も配信しています。
データ加工後のデータイメージ
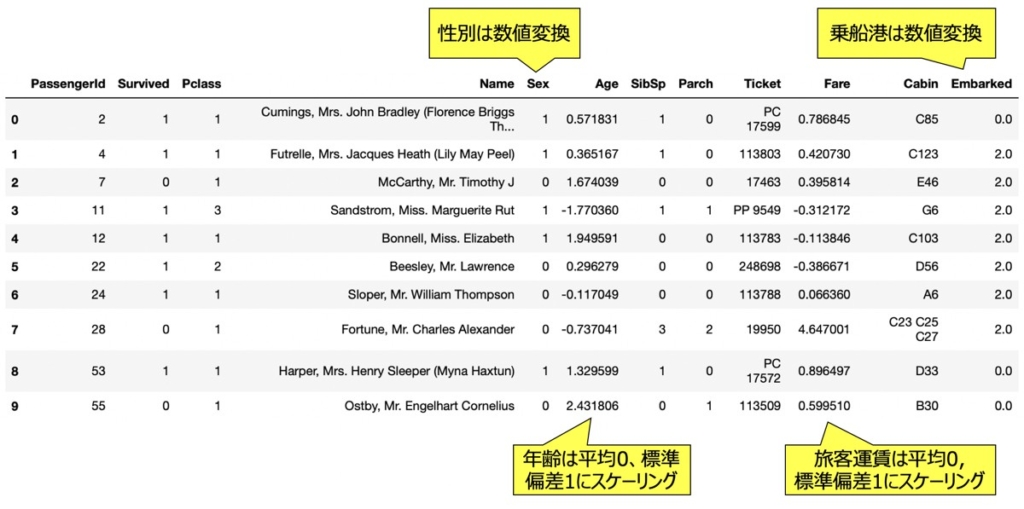
特徴量選択
ロジスティック回帰モデルに用いるインプットとして、説明変数と目的変数をセットします。
今回は次のような変数を選択しています。
| 説明変数 | Pclass, Sex, Age, SibSp, Embarked, Fare |
| 目的変数 | Survived |
説明変数X、目的変数yとした次のようなコードを実行しましょう。
# 説明変数
X = df[["Pclass","Sex","Age","SibSp","Embarked","Fare"]]
# 目的変数
y = df["Survived"]モデル学習|ロジスティック回帰
ロジスティック回帰のインスタンスを作成し、モデル学習を行います。
モデル学習用コード
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# トレーニングデータおよびテストデータ分割
X_train,X_test,Y_train,Y_test = train_test_split(X,y, test_size=0.3, shuffle=True, random_state=3)
# ロジスティック回帰のインスタンス
model = LogisticRegression(penalty='l2', # 正則化項(L1正則化 or L2正則化が選択可能)
dual=False, # Dual or primal
tol=0.0001, # 計算を停止するための基準値
C=1.0, # 正則化の強さ
fit_intercept=True, # バイアス項の計算要否
intercept_scaling=1, # solver=‘liblinear’の際に有効なスケーリング基準値
class_weight=None, # クラスに付与された重み
random_state=None, # 乱数シード
solver='lbfgs', # ハイパーパラメータ探索アルゴリズム
max_iter=100, # 最大イテレーション数
multi_class='auto', # クラスラベルの分類問題(2値問題の場合'auto'を指定)
verbose=0, # liblinearおよびlbfgsがsolverに指定されている場合、冗長性のためにverboseを任意の正の数に設定
warm_start=False, # Trueの場合、モデル学習の初期化に前の呼出情報を利用
n_jobs=None, # 学習時に並列して動かすスレッドの数
l1_ratio=None # L1/L2正則化比率(penaltyでElastic Netを指定した場合のみ)
)
# モデル学習
model.fit(X_train, Y_train)ロジスティック回帰メソッドに指定する引数情報
| 引数名 | 概要 | デフォルト |
|---|---|---|
| penalty | 正則化パラメータを指定。以下の選択肢あり。'none': 正則化パラメータなし'l2': L2正則化'l1': L1正則化'elasticnet': Elastic Net(L1+L2正則化) | ‘l2’ |
| dual | 双対問題(dual)を解くか主問題(primal)を解くか指定。 | 0.5 |
| tol | 計算を停止するための基準値。小さいほど探索に時間を要する。 | 0.0001 |
| C | 正則化の強さを指定。Cの値が小さいほど正則化の強さが増す。 | 1.0 |
| fit_intercept | モデルのバイアス項(切片)を最適化する場合はTrue、しない場合はFalseを指定。 | True |
| intercept_scaling | パラメータ最適化アルゴリズムsolver=‘liblinear’が指定され、 fit_intercept=Trueの際に有効なスケーリング基準値。 | 1 |
| class_weight | クラスに対する重みを辞書形式{class_label:weight}として指定。 指定しない場合、全てのクラスの重みが1になる。 | 1 |
| random_state | 乱数生成器のシードを指定するパラメータ。 | 1000 |
| solver | ハイパーパラメータの最適化の際に使用するアルゴリズム。 ・小さなデータセットの場合は「liblinear」が適切 ・大きなデータセットの場合は「sag」と「saga」が高速。 ・2値ではなく多クラス分類の場合、「newton-cg」「sag」「saga」「lbfgs」のみが多項ロジットを処理可能。 | ‘lbfgs’ |
| max_iter | イテレーションの最大値 | 100 |
| multi_class | 2値分類では’ovr’ 、多クラス分類の場合は’multinomial’を指定。 ‘auto’を指定すれば2値か多クラスか自動で区別してくれる。 | ‘auto’ |
| verbose | liblinearおよびlbfgsがsolverに指定されている場合、冗長性のためにverboseを任意の正の数に設定 | 0 |
| warm_start | Trueの場合、モデル学習の初期化に前の呼出情報を利用。 | False |
| n_jobs | 学習時に並列して動かすスレッドの数。 | False |
| li_ratio | 正則化パラメータpenalty=’elasticnet’の場合に設定するl1/l2正則化の比率。 | None |
正則化について詳しく知りたい方向けに次のような記事も配信しています。
【AI・機械学習】正則化とは|L1・L2正則化の概要解説
機械学習モデル開発において、過学習対策として取り扱われる「正則化」について詳しく解説します。「正則化とは?」「L1・L2正則化って何?」という疑問にお応えします。
モデルの学習結果確認
前述のモデルの学習結果について考察してみましょう。
偏回帰係数の確認
モデルの偏回帰係数は以下で確認できます。偏回帰係数の絶対値が大きい程、その説明変数がモデルの精度向上に際して重要な役割を果たしていることを意味します。重要度の低い説明変数の係数は、その説明変数の影響を打ち消すために0に近い値を取るのが特徴です。
df_model = pd.DataFrame(index=["Pclass","Sex","Age","SibSp","Embarked","Fare"])
df_model["偏回帰係数"] = model.coef_[0]
# 出力イメージ
# 偏回帰係数
# b1 Pclass -0.418780
# b2 Sex 2.363631
# b3 Age -0.607834
# b4 SibSp 0.195629
# b5 Embarked -0.428897
# b6 Fare 0.015289バイアス項(切片)の確認
print("intercept: ", model.intercept_)
# 出力イメージ
# intercept: [1.0597535]モデル推論
前述のロジスティック回帰モデルにテストデータを渡し、予測値を得るための方法を解説します。
目的変数の正事象の発生確率を出力値する方法
タイタニックでの生存率を確率で出力値したい場合は、次のように記述します。
# 確率算出の際は、predict_proba()メソッドを利用
Y_pred_proba = model.predict_proba(X_test)
# データ出力
df_proba = pd.DataFrame()
df_proba["非生存率(Surviced=0)"] = Y_pred_proba[:,0]
df_proba["生存率(Surviced=1)"] = Y_pred_proba[:,1]
print(df_proba)
# 出力イメージ
# 非生存率(Surviced=0) 生存率(Surviced=1)
# 0 0.715506 0.284494
# 1 0.070686 0.929314
# 2 0.327845 0.672155
# 3 0.108550 0.891450
# 4 0.065910 0.934090
# 5 0.294308 0.705692
# 6 0.536102 0.463898
# 7 0.055910 0.944090
# 8 0.123385 0.876615
# 9 0.176352 0.823648
# 10 0.024932 0.9750682値(0または1)で結果を出力する方法
# 推論
Y_pred = model.predict(X_test)
print(Y_pred)
# 出力イメージ
# [0 1 1 1 1 1 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 1 1 1 1 1
# 1 1 0 1 0 0 0 1 1 1 1 1 1 1 0 1 0 0 1 0 0 0 0 0 1 1 0]上記は別解として次のように記載しても同じ結果が得られます。
# 推論
model.predict_proba(X_test).argmax(axis=1)モデル性能評価|ロジスティック回帰
この章では前述で作成したモデルの性能評価方法について解説します。
混合行列・正解率・適合率・再現率・F1の評価
以下代表的な評価指標を用いて学習済みモデルを評価します。
混合行列
from sklearn.metrics import confusion_matrix
# 混合行列
print(confusion_matrix(y_true=Y_test, # 実測値
y_pred=Y_pred # 予測値
))
# 出力イメージ
# [[ 9 9]
# [12 25]]混合行列・正解率・適合率・再現率
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 正解率
print('accuracy: ', round(accuracy_score(y_true=Y_test, y_pred=Y_pred),2))
# 適合率
print('precision: ', round(precision_score(y_true=Y_test, y_pred=Y_pred),2))
# 再現率
print('recall: ', round(recall_score(y_true=Y_test, y_pred=Y_pred),2))
# f1スコア
print('f1 score: ', round(f1_score(y_true=Y_test, y_pred=Y_pred),2))
# 出力イメージ
# accuracy: 0.62
# precision: 0.74
# recall: 0.68
# f1 score: 0.7【参考】上記指標のレポート出力
from sklearn.metrics import classification_report
# 分類問題における評価レポート
print(classification_report(Y_test, Y_pred))
# 出力イメージ
# precision recall f1-score support
# 0 0.43 0.50 0.46 18
# 1 0.74 0.68 0.70 37
# accuracy 0.62 55
# macro avg 0.58 0.59 0.58 55
# weighted avg 0.63 0.62 0.62 55前述した機械学習の分類問題の評価指標について詳しく知りたい方向けに、次のような記事も配信しています。
【AI・機械学習】分類モデルの性能評価および評価指標の解説|正解率・適合率・再現率・F値・特異度・偽陽性率
機械学習における分類モデルの性能評価方法について解説します。本記事読了いただくことで、機械学習の集計データに基づきモデルを多様な角度から評価することができるようになります。
ROC曲線
ロジスティック回帰モデルを用いてROC曲線を描き、AUCを評価した結果を示します。
ROC曲線:コード
ROC曲線を可視化する場合、次のように記述します。
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
# テストデータがクラス1(Survived=1)に属する確率
Y_score = model.predict_proba(X_test)[:, 1]
# ROC曲線の算出(左から偽陽性率:FPR、再現率:TPR、閾値:thresholds)
FPR, TPR, thresholds = roc_curve(y_true=Y_test, y_score=Y_score)
# 理想線
plt.plot([0, 0, 1], [0, 1, 1], linestyle='--', label='Ideal')
# ランダムな推定線
plt.plot([0, 1], [0, 1], linestyle='--', label='Random')
# ROC曲線
plt.plot(FPR, TPR, label='ROC(area = %0.2f)' % auc(FPR, TPR))
plt.legend()
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()ROC曲線:出力イメージ
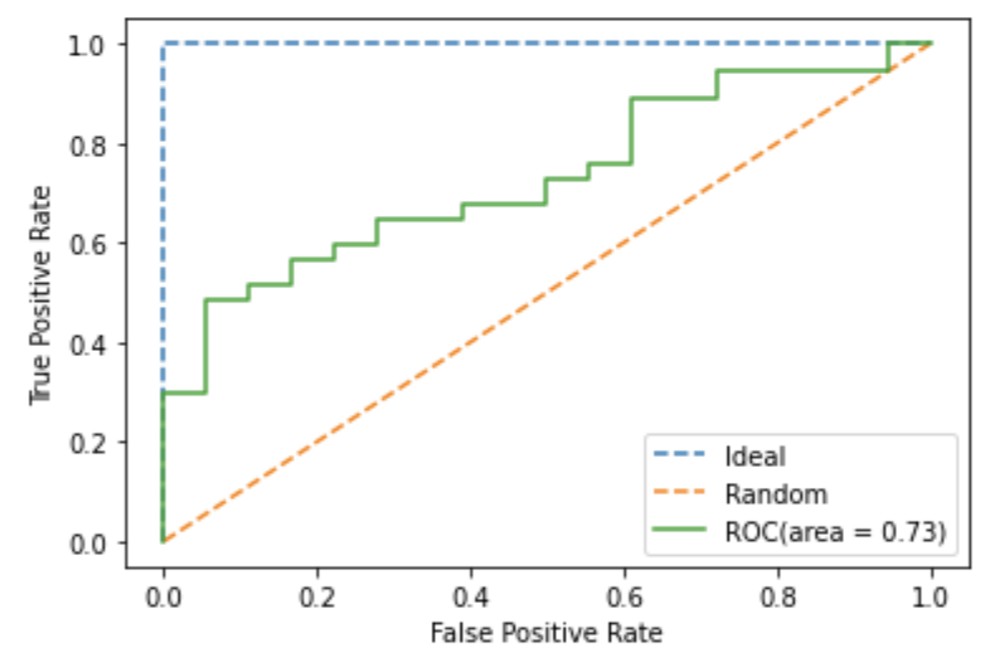
また、AUCは次のように記述しても算出可能です。
from sklearn.metrics import roc_auc_score
# AUC
print('AUC: ', roc_auc_score(y_true = Y_test, # 実測値
y_score = model.predict_proba(X_test)[:, 1] # クラスラベル正事象の発生確率
))
# 出力イメージ
# AUC: 0.73ROC曲線およびAUCについて詳しく知りたい方向けに次のような記事も解説しています。
【AI・機械学習】ROC曲線・PR曲線・AUC|2値分類モデルの性能評価方法を解説!
本記事では機械学習分類モデルの評価指標として用いる「ROC曲線」「PR曲線」「AUC」それぞれの意味・違い・評価方法を詳しく解説します。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




