こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
ナイーブベイズ分類とは|Naive Bayes
確率変数X = (X1, X2, ・・・, Xn)が独立である時、次のような公式が成り立ちます。
P(X1=x1 , X2=x2 , ・・, Xn=xn) = P(X1=x1)P(X2=x2)・・P(Xn=xn)
ここで、Yの条件のもとで確率変数Xが独立であると仮定した場合、次のような条件付き確率が成り立ちます。
P(X1=x1 , X2=x2 , ・・, Xn=xn | Y=y) = P(X1=x1 | Y=y)P(X2=x2 | Y=y)・・P(Xn=xn | Y=y)
この条件付き確率を計算し、Yのカテゴリを分類することをナイーブベイズ分類と言います。
【参考】条件付き確率とベイズの定理
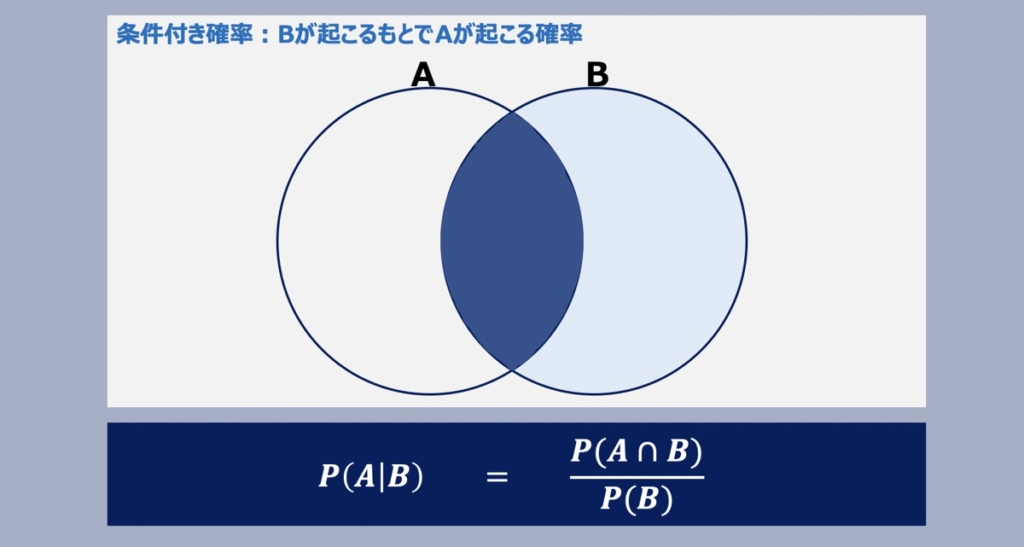
ナイーブベイズ分類の原理は上記に示す条件付き確率がベースで成り立っています。条件付き確率について詳しく知りたい方は、こちらの記事をご覧下さい。
【統計学】条件付き確率とベイズの定理
確率統計学における「条件付き確率」と「ベイズの定理」について詳しく解説しています。理解促進のため「事象と確率」についても概説しています。
ベイズ分類の活用事例
ナイーブベイズ分類によるスパムメールフィルタを例とし、具体的な分類プロセスをイメージ化してみましょう。スパムメールにありそうな単語の集合を次のように定めます。
スパムメール要素 = (お買い得, 当選, 期間限定, 大セールス, ・・・)
続いて、スパムメールフィルタの際に用いる変数を次のように定義します。
- 確率変数Xi:メールの中にi番目の単語がある場合「1」とし、ない場合「0」とする
- 確率変数Y:メールがスパムメールである場合「1」とし、ない場合「0」とする
スパムメールの中に、i番目の単語が入っている確率は次のように表されます。
P(Xi = 1 | Y = 1)
反対に、正常なメールの中に、i番目の単語が入っている確率は次のように表されます。
P(Xi = 1 | Y = 0)
ここで、スパムメール/正常メールの中に、迷惑メール要素の1番目の単語「お買い得」、2番目の単語「当選」、i番目の単語「大セールス」が入っていた場合、スパムメールである場合の条件付き確率と正常メールである場合の条件付き確率は、次のように表されます。
P(X1=1 , X2=1 , ・・, Xi=1 | Y=1) = P(X1=1 | Y=1)P(X2=1 | Y=1)P(Xi=1 | Y=1)
P(X1=1 , X2=1 , ・・, Xi=1 | Y=0) = P(X1=1 | Y=0)P(X2=1 | Y=0)P(Xi=1 | Y=0)
①, ②を計算し、①の確率が高ければスパムメールであると判定し、低ければ迷惑メールでは無いと判定します。
ナイーブベイズ分類は上記のような確率計算をもとに成り立つモデルとイメージしましょう。
ナイーブベイズ分類アルゴリズムの特徴
ナイーブベイズアルゴリズムとは、ベイズの定理をもとに確率を掛け合わせ、最終的な分類結果を出力するアルゴリズムです。次のような特徴を持ちます。
特徴
- 与えられたデータに対して推定の条件付き確率を計算、最も確率の高い結果を出力
- 外れ値の影響を受けずらい
- 非線形の問題にも対応可能
- 少ないトレーニングデータでも性能を発揮
注意点
- 特徴量が互いに独立していることが前提
scikit-learnで実装可能なナイーブベイズ分類アルゴリズム
scikit-learnを用いて実装可能なナイーブベイズ分類アルゴリズムとして、以下3つがあります。
| アルゴリズム名 | 特徴 |
|---|---|
| ガウシアンナイーブベイズ | ・特徴ベクトルに正規分布を仮定 ・連続値である説明変数に対応 ・平均と分散を用いた確率密度関数を用い確率を計算 |
| 多項ナイーブベイズ | ・特徴ベクトルに多項分布を仮定 ・連続値である説明変数に対応 |
| ベルヌーイナイーブベイズ | ・特徴ベクトルにベルヌーイ分布を仮定 ・離散型の説明変数を用いる際に有効 ・説明変数をバイナリ変数に変換して確率を計算 |
【Python】scikit-learnを用いたナイーブベイズ分類モデルの開発
Python環境下でscikit-learnという機械学習ライブラリを用い、ナイーブベイズ分類モデルを構築する方法について解説します。以下の手順に従い、モデルを構築していきましょう。
- データセットの説明
- データの準備
- Naive Bayes分類モデル学習
- モデル推論
- モデル評価
データセットの説明

データセットには、機械学習のサンプルデータとして有名なIris(アヤメ)データセットを活用します。3種類のアヤメ(Iris Setosa, Iris Versicolor, Iris Virginica)があり、それぞれ50サンプルずつ(合計150サンプル)用意されているデータです。このアヤメの名前を目的変数として利用します。また、説明変数にはアヤメの計測値である萼片(sepals)と花びら(petals)の長さと幅の4つを利用します。
データの準備
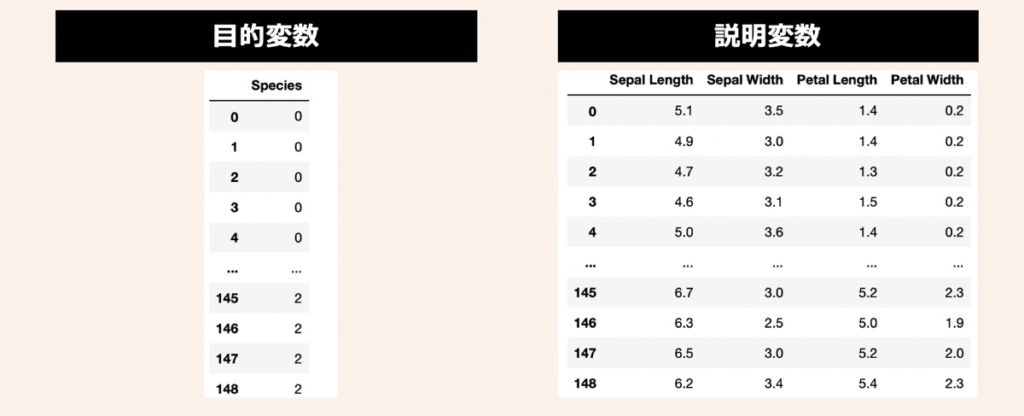
まず、前述したアヤメのデータセットを準備します。上記目的変数と説明変数をPandas形式で取り扱うために、下記のコードを実行してみましょう。
"""
①データセットの準備(Sckit-learnで提供されているアヤメのデータを利用)
"""
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
# データロード
iris = datasets.load_iris()
# 説明変数
X = iris.data
X = pd.DataFrame(X, columns=["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"])
# 目的変数
Y = iris.target
Y = iris_target = pd.DataFrame(Y, columns = ["Species"])
# 学習データとテストデータ分割
X_train,X_test,Y_train,Y_test = train_test_split(X,Y, test_size=0.3, shuffle=True, random_state=3)モデル学習①|Gaussian Naive Bayes
GaussianNB()メソッドを用いてガウシアンナイーブベイズ分類モデルを作成する方法です。
# Gaussian Naive Bayes
from sklearn.naive_bayes import GaussianNB
GNB_model = GaussianNB(priors=None, # 各クラスの事前確率を指定するかどうか
var_smoothing=1e-09) # 計算の安定性のため左記値を分散項目に追加
# モデル学習
GNB_model.fit(X_train,Y_train)
# モデルパラメータ確認
GNB_model.get_params(deep=True)モデル学習②|Multinomial naive Bayes
MultinomialNB()メソッドを用いて多項ナイーブベイズ分類モデルを作成する方法です。
# Multinomial naive Bayes
from sklearn.naive_bayes import MultinomialNB
MNB_model = MultinomialNB(alpha=1.0, # ラプラススムージングのパラメーター(ゼロ頻度問題対策)
fit_prior=True, # Trueの場合はクラスの事前確率を計算
class_prior=None) # 上記Trueの場合、各クラスの事前確率をタプル形式で指定
# モデル学習
MNB_model.fit(X_train,Y_train)
# モデルパラメータ確認
MNB_model.get_params(deep=True)モデル学習③|Bernoulli naive Bayes
BernoulliNB()メソッドを用いてベルヌーイナイーブベイズ分類モデルを作成する方法です。
# Bernoulli naive Bayes
from sklearn.naive_bayes import BernoulliNB
BNB_model = BernoulliNB(alpha=1.0, # ラプラススムージングのパラメーター(ゼロ頻度問題対策)
binarize=0.0, # 2値化の閾値(閾値値を超える値を1、それ以外を0に分類)
fit_prior=True, # Trueの場合はクラスの事前確率を計算
class_prior=None) # 上記Trueの場合、各クラスの事前確率をタプル形式で指定
# モデル学習
BNB_model.fit(X_train,Y_train)
# モデルパラメータ確認
BNB_model.get_params(deep=True)【Python】ナイーブベイズ分類モデルによる推論・性能評価
前述で作成した分類モデルを用いた推論方法と性能評価方法について解説します。
モデル推論
前述で作成した3つのナイーブベイズモデルの推論結果について観察してます。
モデル推論結果を出力するメソッドには以下が利用できます。
| predict() | クラスラベルを推論結果として出力 |
| predict_proba() | 各クラスの発生確率を推論結果として出力 |
| predict_log_proba() | 上記に対数を取った値を推論結果として出力 |
今回はpredict()メソッドを用いて結果を観察します。
Gaussian Naive Bayes
# ガウシアンナイーブベイズ
Y_pred_GNB = GNB_model.predict(X_test)
print(Y_pred_GNB)
# 出力結果
# [0 0 0 0 0 2 1 0 2 1 1 0 1 1 2 0 1 2 2 0 2 2 2 1 0 2 2 1 1 1 0 0 2 1 0 0 2 0 2 1 2 1 0 0 2]Multinomial naive Bayes
# 多項ナイーブベイズ
Y_pred_MNB = MNB_model.predict(X_test)
print(Y_pred_MNB)
# 出力結果
# [0 0 0 0 0 2 1 0 2 1 1 0 1 1 2 0 2 2 2 0 2 2 2 1 0 2 2 1 1 1 0 0 2 1 0 0 1 0 2 2 2 1 0 0 2]Bernoulli naive Bayes
# ベルヌーイナイーブベイズ
Y_pred_BNB = BNB_model.predict(X_test)
print(Y_pred_BNB)
# 出力結果
# [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]今回の場合、モデル学習に用いた説明変数はバイナリ化できる変数ではないため、ベルヌーイナイーブベイズ分類モデルは上手く機能していないことが分かります。
モデル性能評価
ガウシアンナイーブベイズアルゴリズムと多項ナイーブベイズアルゴリズムをもとに作成したモデルの性能評価を行います。
Gaussian Naive Bayes
from sklearn.metrics import classification_report
# 評価レポート
print(classification_report(Y_test, Y_pred_GNB))
# 出力結果
# precision recall f1-score support
# 0 1.00 1.00 1.00 17
# 1 1.00 0.93 0.96 14
# 2 0.93 1.00 0.97 14
# accuracy 0.98 45
# macro avg 0.98 0.98 0.98 45
# weighted avg 0.98 0.98 0.98 45Multinomial naive Bayes
from sklearn.metrics import classification_report
# 評価レポート
print(classification_report(Y_test, Y_pred_MNB))
# 出力結果
# precision recall f1-score support
# 0 1.00 1.00 1.00 17
# 1 1.00 0.86 0.92 14
# 2 0.88 1.00 0.93 14
# accuracy 0.96 45
# macro avg 0.96 0.95 0.95 45
# weighted avg 0.96 0.96 0.96 45【参考】Python×統計学の学習におすすめな教材
「データ分析する上で重要な統計基礎を学びたい」「Pythonで動かしながら本格的に機械学習モデルを構築したい」方向けに以下の教材をおすすめします。
データ分析で必須の統計学基礎を学びたい方向け
Pythonで本格的に機械学習モデルを構築してみたい方向け
Pythonで実際に動かしながら学習することで、プログラミングに加え、統計学・機械学習の概念理解も合わせて実施できます。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら






