こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- ランダムフォレスト回帰のモデル学習および評価方法について詳しく知りたい
- 上記アルゴリズムをPythonで実装できるようになりたい
ランダムフォレストとは
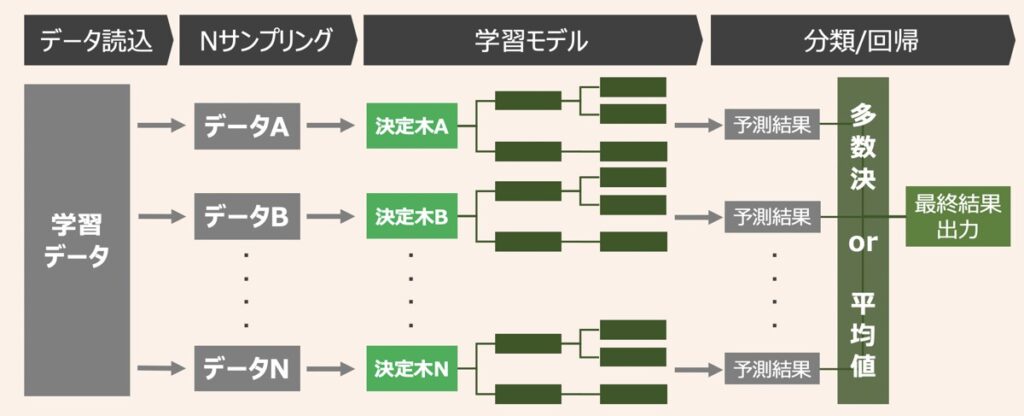
ランダムフォレストとは、決定木による複数識別器を統合させたバギングベースのアンサンブル学習アルゴリズムです。分類(判別)・回帰(予測)両方の用途で利用可能な点も特徴的です。
ランダムフォレストは、決定木モデルを単体で利用した場合に発現しやすい過学習問題に対応した方法の1つとして位置付けられます。復元抽出したデータで過学習した決定木を複数用意し、各決定木から得られた結果を多数決または平均値を取ることで最終結果を得ます。このような仕組みを利用することで過学習の度合いを減らそうという思想です。
本記事ではPythonを用いてランダムフォレストの回帰モデルの作成・評価方法について解説します。
【事前準備】ランダムフォレスト回帰モデル作成に必要なデータ
実際にPythonのScikit-learnライブラリを用いてランダムフォレストの回帰モデルを構築していきましょう!下記の手順でプログラムを構築していきます。
- データセットの説明
- データの準備
- 回帰モデル学習
- モデル性能評価
今回は機械学習モデル過程で必須となるデータクレンジングやグラフ可視化等の前処理プロセスは割愛しています。その代わり、モデル作成と評価方法を詳しく解説しております。
データクレンジングやグラフ可視化を通じて回帰モデル作成について言及した記事も配信しています。合わせてご覧下さい。
【機械学習・Python】線形単回帰・重回帰分析に基づき予測モデルを作成|scikit-learnでモデル開発・評価
Pythonとscikit-learnを用いて単回帰および重回帰モデルを作成・評価する方法について解説します。
データセットの説明

データセットには、Boston Housingというデータセットを活用します。
1970年代後半におけるボストンの住宅情報とその地域における環境をまとめたデータセットであり、住宅価格の予測を目的とした回帰モデル作成のチュートリアルによく利用されます。
Boston Housingデータセットの説明変数および目的変数の概要はそれぞれ以下になります。
説明変数一覧
| 特徴量名 | 概要 |
|---|---|
| CRIM | (地域人工毎の)犯罪発生率 |
| ZN | 25,000平方フィート以上の住宅区画の割合 |
| INDUS | (地域人工毎の)非小売業の土地面積の割合 |
| CHAS | チャールズ川沿いに立地しているかどうか(該当の場合は1、そうでない場合は0) |
| NOX | 窒素酸化物の濃度(単位:pphm) |
| RM | 平均部屋数/一戸 |
| AGE | 1940年よりも古い家の割合 |
| DIS | 5つのボストン雇用センターまでの重み付き距離 |
| RAD | 主要な高速道路へのアクセス指数 |
| TAX | 10,000ドルあたりの所得税率 |
| PTRATIO | (地域人工毎の)学校教師1人あたりの生徒数 |
| B | (地域人工毎の)アフリカ系アメリカ人居住者の割合 |
| LSTAT | 低所得者の割合 |
目的変数一覧
| 特徴量名 | 概要 |
|---|---|
| MEDV | 住宅価格の中央値(単位 $1,000) |
データの準備
前述したBoston Housingのデータセットを準備するために以下のコードを実行しましょう。
# データ前処理
import numpy as np
import pandas as pd
# データ可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("ggplot")
# %matplotlib inline
# グラフの日本語表記対応
from matplotlib import rcParams
rcParams["font.family"] = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"
# データセット読込
from sklearn.datasets import load_boston
boston = load_boston()
# DataFrame作成
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df["MEDV"] = boston.target【実践】ランダムフォレスト回帰モデルの作成・評価|単回帰の場合
ランダムフォレストの回帰モデル作成に際して、次のような変数を用います。
まずは分かりやすいように、単回帰のモデルを作成します。
| 説明変数 | LSTAT(低所得者の割合) |
| 目的変数 | MEDV(住宅価格の中央値) |
【モデル学習】ランダムフォレスト回帰
ランダムフォレストの回帰モデルを作成するコードを下記に示します。
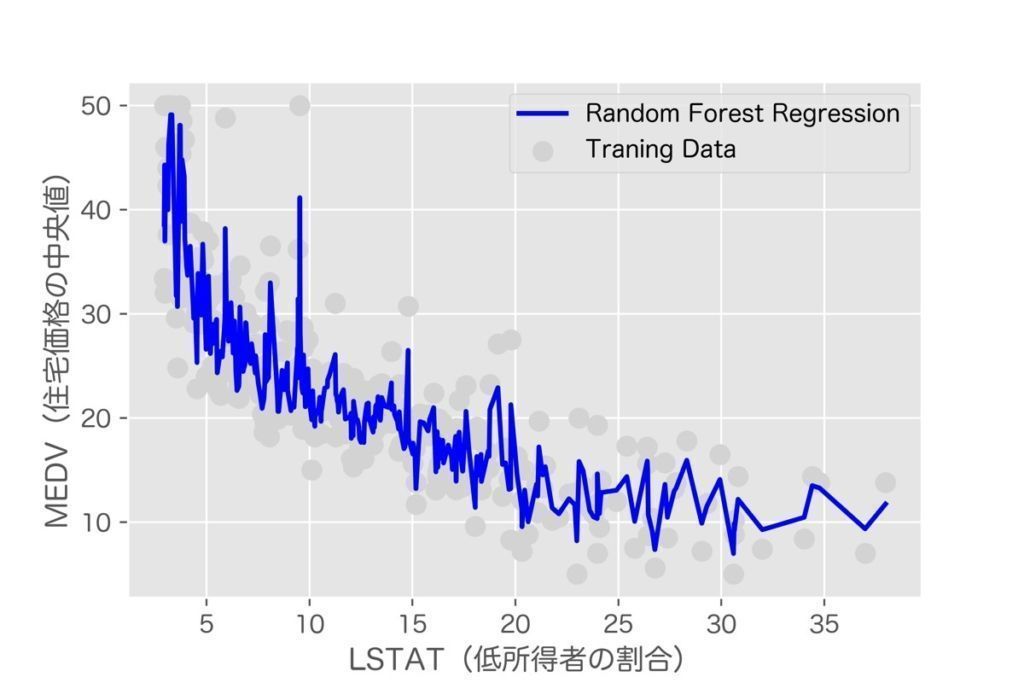
加えて、推論結果の可視化も合わせて行います。
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
""" モデル学習 """
# 変数定義
X = df[['LSTAT']].values # 説明変数
y = df['MEDV'].values # 目的変数(住宅価格の中央値)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
# ランダムフォレスト回帰
forest = RandomForestRegressor(n_estimators=100,
criterion='mse',
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
bootstrap=True,
oob_score=False,
n_jobs=None,
random_state=None,
verbose=0,
warm_start=False,
ccp_alpha=0.0,
max_samples=None
)
# モデル学習
forest.fit(X_train, y_train)
# 推論
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
""" グラフ可視化 """
# flatten:1次元の配列を返す、argsort:ソート後のインデックスを返す
sort_idx = X_train.flatten().argsort()
# 可視化用に加工
X_train_plot = X_train[sort_idx]
Y_train_plot = y_train[sort_idx]
train_predict = forest.predict(X_train_plot)
# 可視化
plt.scatter(X_train_plot, Y_train_plot, color='lightgray', s=70, label='Traning Data')
plt.plot(X_train_plot, train_predict, color='blue', lw=2, label="Random Forest Regression")
# グラフの書式設定
plt.xlabel('LSTAT(低所得者の割合)')
plt.ylabel('MEDV(住宅価格の中央値)')
plt.legend(loc='upper right')
plt.show()RandomForestRegressorメソッドの概要
ランダムフォレスト回帰は、scikit-learnのRandomForestRegressor()メソッドを用いて作成できます。
このメソッドで利用する引数情報を下記に示します。
forest = RandomForestRegressor(n_estimators=100,
criterion='mse',
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
bootstrap=True,
oob_score=False,
n_jobs=None,
random_state=None,
verbose=0,
warm_start=False,
ccp_alpha=0.0,
max_samples=None
)| 引数名 | 概要 | デフォルト |
|---|---|---|
| n_estimators | バギングに用いる決定木の数 | 100 |
| criterion | 不純度を測定する基準(平均二乗誤差、平均絶対誤差など) | ‘squared_error’ |
| max_depth | 決定木のノード深さの制限値。ツリーが深くなりすぎて過学習の状態に陥った際は、このパラメータが正則化の役割を果たす | None |
| min_samples_split | ノードを分岐に必要なデータの最小値。サンプルが最小値を下回った場合、葉ノードとなる | 2 |
| min_samples_leaf | 葉ノードの作成に必要なデータ数の最小値。指定した値以上のデータ数を持たない葉ノードは作られない | 1 |
| min_weight_fraction_leaf | サンプルの重みを考慮した上でのmin_samples_leafに該当 | 0.0 |
| max_features | ランダムに指定する説明変数の数。(全ての説明変数がモデル学習に活用されるわけではなく、ランダムに割り振られる) | ‘auto’ |
| max_leaf_nodes | 作成する葉ノードの最大値 | None |
| min_impurity_decrease | 決定木の成長の早期停止するための閾値。不純度が指定の値より減少した場合、ノードを分岐し、不純度が指定の値より減少しなければ分岐を抑制。 | 0.0 |
| bootstrap | 決定木モデル作成時におけるブートストラップサンプリングの実行要否 | True |
| oob_score (out-of-bag) | 各ブートストラップサンプリングにて抽出されなかったサンプルの利用要否 | False |
| n_jobs | モデル学習・予測に用いるスレッド数 | None |
| random_state | 乱数シード | None |
| verbose | モデル作成過程でメッセージを表示するかどうか | 0 |
| warm_start | Trueの場合はフィット(演算)し終えたモデルに追加の学習が可能 | False |
| ccp_alpha | 剪定パラメータ(コスト複雑度枝刈り)ccp_alpha の値が大きいほど剪定されるノード数が増えるため、シンプルなツリーが形成される | 0.0 |
| max_samples | bootstrapがTrueの場合、サンプリングする最大値を指定 | None |
【評価】RMSEおよび決定係数R2を用いた性能評価
RMSE(平均平方二乗誤差)と決定係数R2を用いて回帰モデルの性能を評価します。
from sklearn.metrics import r2_score # 決定係数
from sklearn.metrics import mean_squared_error # RMSE
# 予測値(Train)
y_train_pred = forest.predict(X_train)
# 予測値(Test)
y_test_pred = forest.predict(X_test)
# 平均平方二乗誤差(RMSE)
print('RMSE 学習: %.2f, テスト: %.2f' % (
mean_squared_error(y_train, y_train_pred, squared=False), # 学習
mean_squared_error(y_test, y_test_pred, squared=False) # テスト
))
# 決定係数(R^2)
print('R^2 学習: %.2f, テスト: %.2f' % (
r2_score(y_train, y_train_pred), # 学習
r2_score(y_test, y_test_pred) # テスト
))
# 出力結果
# RMSE 学習: 2.37, テスト: 6.72
# R^2 学習: 0.93, テスト: 0.50上記決定係数R2に着目すると、学習データを用いたR2は0.93と非常に関係が捕捉できたが、テストデータを用いたR2は0.50と低いことが分かります。
この結果から、ランダムフォレスト回帰のモデルは、学習データに過剰フィットした過学習の状態にあると言えます。
ここで回帰モデルの評価指標について詳しく知りたい方はこちらの記事で解説しています。
【AI・機械学習】回帰モデルの性能評価および評価指標の解説|決定係数・RMSE・MAE・残差プロット
機械学習の性能評価方法の中で「回帰モデルはどうやって評価するの?」本記事ではその疑問に回答します。具体的に、決定係数、RMSE、MAE等の評価指標があり、それら特徴・利用シーンを1つずつ詳しく解説します。
【評価】残差プロットによる可視化
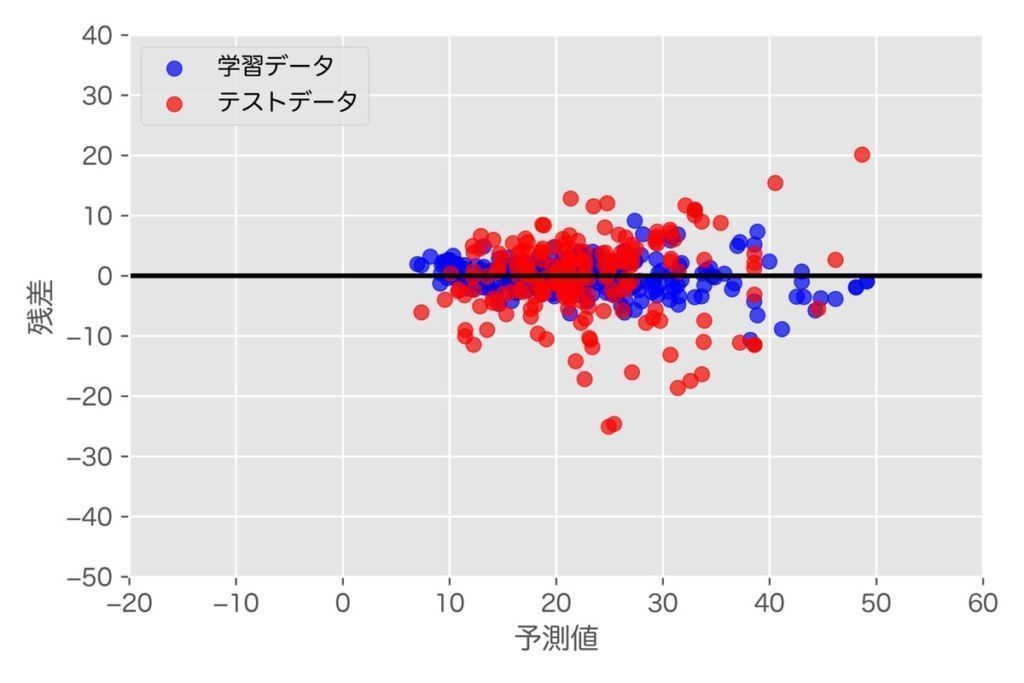
ランダムフォレスト回帰の性能評価として残差プロットを用いる場合、下記のコードを実行します。
残差プロットからも過学習の兆候が見てとれます。学習データからなる予測性能誤差のプロットは、残差0近辺に分布していますが、テストデータのそれはまばらに分布しており、予測性能誤差もそれぞれ大きいことが分かります。
# 予測値と残差をプロット(学習データ)
plt.scatter(y_train_pred, # グラフのx値(予測値)
y_train_pred - y_train, # グラフのy値(予測値と学習値の差)
c='blue', # プロットの色
marker='o', # マーカーの種類
s=40, # マーカーサイズ
alpha=0.7, # 透明度
label='学習データ') # ラベルの文字
# 予測値と残差をプロット(テストデータ)
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='red',
marker='o',
s=40,
alpha=0.7,
label='テストデータ')
# グラフの書式設定
plt.xlabel('予測値')
plt.ylabel('残差')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-20, xmax=60, lw=2, color='black')
plt.xlim([-20, 60])
plt.ylim([-50, 40])
plt.tight_layout()
plt.show()【実践】ランダムフォレスト回帰モデルの作成・評価|重回帰の場合
続いて複数の説明変数をランダムフォレスト回帰に適用し、モデルを作成・評価します。加えて、単回帰の場合と性能を比較してみましょう。
| 説明変数 | 目的変数以外の変数全て |
| 目的変数 | MEDV |
【モデル学習】ランダムフォレスト回帰
ランダムフォレスト回帰のモデル学習に用いるコードを下記に示します。
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
""" モデル学習 """
# 変数定義
X = df.iloc[:, :-1].values # 説明変数(目的変数以外)
y = df['MEDV'].values # 目的変数(住宅価格の中央値)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
# ランダムフォレスト回帰
forest = RandomForestRegressor(n_estimators=100,
criterion='mse',
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
bootstrap=True,
oob_score=False,
n_jobs=None,
random_state=None,
verbose=0,
warm_start=False,
ccp_alpha=0.0,
max_samples=None
)
# モデル学習
forest.fit(X_train, y_train)【評価】RMSEおよび決定係数R2を用いた性能評価
RMSE(平均平方二乗誤差)と決定係数R2を用いて回帰モデルの性能を評価します。
from sklearn.metrics import r2_score # 決定係数
from sklearn.metrics import mean_squared_error # RMSE
# 予測値(Train)
y_train_pred = forest.predict(X_train)
# 予測値(Test)
y_test_pred = forest.predict(X_test)
# 平均平方二乗誤差(RMSE)
print('RMSE 学習: %.2f, テスト: %.2f' % (
mean_squared_error(y_train, y_train_pred, squared=False), # 学習
mean_squared_error(y_test, y_test_pred, squared=False) # テスト
))
# 決定係数(R^2)
print('R^2 学習: %.2f, テスト: %.2f' % (
r2_score(y_train, y_train_pred), # 学習
r2_score(y_test, y_test_pred) # テスト
))
# 出力結果
# RMSE 学習: 1.28, テスト: 3.33
# R^2 学習: 0.98, テスト: 0.88決定係数R2に着目すると、学習データを用いて算出したR2は0.93→0.98、テストデータより算出したR2は0.50→0.88であり、単回帰の場合と比較して大きく精度が改善されています。
さらに、テストデータより算出したR2も1に近い値を示したことから、汎化性能も良いと言えます。
【評価】残差プロットによる可視化
最後に、ランダムフォレスト回帰の残差プロットを示します。

# 予測値と残差をプロット(学習データ)
plt.scatter(y_train_pred, # グラフのx値(予測値)
y_train_pred - y_train, # グラフのy値(予測値と学習値の差)
c='blue', # プロットの色
marker='o', # マーカーの種類
s=40, # マーカーサイズ
alpha=0.7, # 透明度
label='学習データ') # ラベルの文字
# 予測値と残差をプロット(テストデータ)
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='red',
marker='o',
s=40,
alpha=0.7,
label='テストデータ')
# グラフの書式設定
plt.xlabel('予測値')
plt.ylabel('残差')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-20, xmax=60, lw=2, color='black')
plt.xlim([-20, 60])
plt.ylim([-50, 40])
plt.tight_layout()
plt.show()【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




