こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- RANSACアルゴリズムを用いたロバスト回帰モデルについて詳しく知りたい
- 上記アルゴリズムをPythonで実装できるようになりたい
RANSACアルゴリズムを用いたロバスト回帰分析とは
本記事では、PythonによるRANSACアルゴリズムを用いたロバスト回帰モデルの構築方法について詳しく解説して行きます。その前段階として、そもそもロバスト回帰およびRANSACとは何か解説します。
ロバスト回帰
最小二乗法の欠点として、データサンプルの中に外れ値が存在した場合、回帰モデルの性能が著しく低下してしまうことがあります。最小二乗法では、誤差の2乗を計算に用いるため、外れ値が大きいと誤差関数も大きくなるのが原因です。
ロバスト回帰とは、上記背景を鑑み、外れ値の影響を受けにくくなるよう設計された回帰モデルを指します。
ロバスト回帰は、最小二乗法の適用過程で外れ値の情報(重み)を付与することで、導出する回帰モデルが外れ値の影響を受けにくくなるような仕組みを導入しています。
ここで、回帰分析の理論的な概要が知りたい方はこちらの記事で解説していますため、合わせてご覧下さい。
線形単回帰・重回帰分析とは?|回帰モデル導出・評価における統計学的理論や機械学習への応用方法を徹底解説
「単回帰・重回帰分析の概要」「回帰モデル作成時の評価方法やモデル性能改善方法」について詳しく知りたい方向けの記事です。
RANSAC(RANdom SAmple Consensus)
ロバスト回帰の中の代表的な手法として、RANSAC(Random Sample Consensus)があります。
RANSACは、まず、外れ値を含むデータセットからデータをランダム抽出し、回帰モデルの作成し、正常値に該当するデータの割合を求めます。次に、そのプロセスを繰り返し、新たに作成した回帰モデルから正常値の割合を算出・前プロセスの結果と比較します。最終的に最も正常値の割合が高くなった回帰モデルを採用するといった流れです。
ここで、正常値と外れ値を識別する閾値はモデル開発者が設定します。回帰モデルの場合、デフォルトでは目的変数の中央絶対偏差(Mean Absolute Deviation)がしばし用いられます。
RANSACを機械学習アルゴリズムとして適用すると、以下のように反復学習が進行します。
- データセットからランダムなサンプル数をピックアップ
- 選択したサンプルを用いてモデルを学習・評価
- モデル開発者が指定した正常値の範囲に該当するサンプルを追加
- 正常値に該当する全てのサンプルを用いてモデルを再び学習
- 2と4をもとに、正常値に対する学習済みモデルの誤差を算出
- モデルの性能がモデル開発者が指定した許容範囲を満たした場合、またはイテレーション数が規定に到達した場合、学習を終了。これらに該当しない場合1に戻って反復。
【事前準備】RANDAC・ロバスト回帰モデル作成に必要なデータ
実際にPythonのScikit-learnライブラリを用いてロバスト回帰モデルを構築していきましょう!下記の手順でプログラムを構築していきます。
- データセットの説明
- データの準備
- 回帰モデル学習
- モデル性能評価
回帰モデルの性能を比較するために、単回帰と重回帰モデルを作成し、性能を評価します。
今回は機械学習モデル過程で必須となるデータクレンジングやグラフ可視化等の前処理プロセスは割愛しています。その代わり、モデル作成と評価方法を詳しく解説しております。
データセットの説明

データセットには、Boston Housingというデータセットを活用します。
1970年代後半におけるボストンの住宅情報とその地域における環境をまとめたデータセットであり、住宅価格の予測を目的とした回帰モデル作成のチュートリアルによく利用されます。
Boston Housingデータセットの説明変数および目的変数の概要はそれぞれ以下になります。
説明変数一覧
| 特徴量名 | 概要 |
|---|---|
| CRIM | (地域人工毎の)犯罪発生率 |
| ZN | 25,000平方フィート以上の住宅区画の割合 |
| INDUS | (地域人工毎の)非小売業の土地面積の割合 |
| CHAS | チャールズ川沿いに立地しているかどうか(該当の場合は1、そうでない場合は0) |
| NOX | 窒素酸化物の濃度(単位:pphm) |
| RM | 平均部屋数/一戸 |
| AGE | 1940年よりも古い家の割合 |
| DIS | 5つのボストン雇用センターまでの重み付き距離 |
| RAD | 主要な高速道路へのアクセス指数 |
| TAX | 10,000ドルあたりの所得税率 |
| PTRATIO | (地域人工毎の)学校教師1人あたりの生徒数 |
| B | (地域人工毎の)アフリカ系アメリカ人居住者の割合 |
| LSTAT | 低所得者の割合 |
目的変数一覧
| 特徴量名 | 概要 |
|---|---|
| MEDV | 住宅価格の中央値(単位 $1,000) |
データの準備
前述したBoston Housingのデータセットを準備するために以下のコードを実行しましょう。
# データ前処理
import numpy as np
import pandas as pd
# データ可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("ggplot")
# %matplotlib inline
# グラフの日本語表記対応
from matplotlib import rcParams
rcParams["font.family"] = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"
# データセット読込
from sklearn.datasets import load_boston
boston = load_boston()
# DataFrame作成
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df["MEDV"] = boston.target【実践】RANSAC・ロバスト回帰モデルの作成・評価|単回帰分析
まず、1つの説明変数を用いて線形のロバスト回帰モデルを作成・評価します。
| 説明変数 | RM |
| 目的変数 | MEDV |
回帰モデルの学習
ロバスト回帰モデル作成に用いるコードを下記に示します。推論結果も合わせて可視化しましょう。

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import RANSACRegressor
from sklearn.model_selection import train_test_split
# 変数定義
X = df[['RM']].values # 説明変数
y = df['MEDV'].values # 目的変数
# 学習・テストデータ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# RANSACを用いたロバスト回帰モデル
model_ransac = RANSACRegressor(
base_estimator = LinearRegression(), # ベースモデル
min_samples=50, # ランダムに選択されたデータサンプルの最小数
residual_threshold=8.0, # 正常値として分類されるデータサンプルの最大残差(ここを大きくすると正常値として許容されるサンプル数が増える)
max_trials=200, # イテレーションの最大回数
stop_n_inliers=np.inf, # 左記指定以上の正常値が見つかった場合は、イテレーション停止
stop_score=np.inf, # スコアが左記閾値よりも大きい場合の上位のイテレーション停止
stop_probability=0.99, # トレーニングデータの少なくとも1つの外れ値のないセットがRANSACでサンプリングされると、RANSACのイテレーションは停止
loss='absolute_loss', # 絶対誤差(absolute_loss)または二乗誤差(squared_error)が選択可能
random_state=0 # ランダムシード
)
# モデル学習
model_ransac.fit(X_train, y_train)
inlier = model_ransac.inlier_mask_ # 正常値の場合Trueを返す配列
outlier = np.logical_not(inlier) # 外れ値の場合Trueを返す配列
x_lim = np.arange(2, 11, 1) # 2~11までの配列を作成
pred_ransac = model_ransac.predict(x_lim[:, np.newaxis]) # 上記の配列を整数値に直し、モデルに適用
# 正常値プロット
plt.scatter(X_train[inlier], # 横軸
y_train[inlier], # 縦軸
c='blue', # プロットカラー
edgecolor="black", # プロットカラー(枠線)
s=20, # プロットサイズ
marker='o', # プロット形状
label='正常値') # ラベル
# 外れ値プロット
plt.scatter(X_train[outlier], # 横軸
y_train[outlier], # 縦軸
c='green', # プロットカラー
edgecolor='black', # プロットカラー(枠線)
s=30, # プロットサイズ
marker='o', # プロット形状
label='外れ値' # ラベル
)
# 予測値プロット
plt.plot(x_lim,
pred_ransac,
color='red',
lw=3,
label="回帰直線",
)
# グラフの書式設定
plt.xlim([3,10])
plt.ylim([y.min()-15,y.max()+10])
plt.xlabel('RM')
plt.ylabel('MEDV')
plt.legend(loc='upper left')
plt.show()
# 直線情報
print('傾き: %.2f' % model_ransac.estimator_.coef_[0])
# 出力結果(傾き)
# 11.42
print('切片: %.2f' % model_ransac.estimator_.intercept_)
# 出力結果(切片)
# -49.01ロバスト回帰モデル作成に用いるRANSACRegressorに対して、residual_thresholdという正常値/外れ値の閾値を設定する引数を与えます。
その結果、上図グラフで示すような正常値(青プロット)を学習し、回帰モデルが作成されました。
RANSACアルゴリズムの概要
scikit-learnのRANSACRegressor()メソッドを用いて今回ロバスト回帰モデルを作成しています。
このメソッドで利用する引数情報を下記に示します。
model_ransac = RANSACRegressor(
base_estimator=None,
min_samples=None,
residual_threshold=None,
max_trials=100,
max_skips=inf,
stop_n_inliers=inf,
stop_score=inf,
stop_probability=0.99,
loss='absolute_error',
random_state=None
)| 引数名 | 概要 | デフォルト |
|---|---|---|
| base_estimator | 下記メソッドを実装したオブジェクトを指定。 fit(X, y):モデル学習 score(X, y):性能評価 predict(X):推論 | None |
| min_samples | ランダムに選択されたデータサンプルの最小数 | None |
| residual_threshold | 正常値として分類されるデータサンプルの最大残差 (ここを大きくすると正常値として許容されるサンプル範囲が増加) | 平均絶対偏差(MAD) |
| max_trials | イテレーション最大回数 | 100 |
| stop_n_inliers | 指定した数以上の正常値が見つかった場合、イテレーション停止 | np.inf |
| stop_score | スコアが指定の閾値よりも大きい場合、イテレーション停止 | np.inf |
| stop_probability | 学習データのサブセットがN個のサンプル以下で生成された場合、イテレーション停止 N >= log(1 – probability) / log(1 – e**m) e:正常値の割合 | 0.99 |
| loss | 損失関数。絶対誤差(absolute_loss)または二乗誤差(squared_error)を選択可能。 | absolute_error |
| random_state | 乱数シード | None |
【評価】RMSEおよび決定係数R2を用いた性能評価
RMSE(平均平方二乗誤差)と決定係数R2を用いて回帰モデルの性能を評価します。
from sklearn.metrics import r2_score # 決定係数
from sklearn.metrics import mean_squared_error # RMSE
# 予測値(Train)
y_train_pred = model_ransac.predict(X_train)
# 予測値(Test)
y_test_pred = model_ransac.predict(X_test)
# 平均平方二乗誤差(RMSE)
print('RMSE 学習: %.2f, テスト: %.2f' % (
mean_squared_error(y_train, y_train_pred, squared=False), # 学習
mean_squared_error(y_test, y_test_pred, squared=False) # テスト
))
# 決定係数(R^2)
print('R^2 学習: %.2f, テスト: %.2f' % (
r2_score(y_train, y_train_pred), # 学習
r2_score(y_test, y_test_pred) # テスト
))
# 出力結果
# RMSE 学習: 6.66, テスト: 7.12
# R^2 学習: 0.48, テスト: 0.39上記決定係数R2に着目すると、学習データを使ったR2は0.48、テストデータを使ったR2は0.39であり、性能としてはあまり良くない結果でした。
学習データの決定係数自体がそもそも低いため、学習不足だと分かります。今回用いた説明変数では目的変数がうまく説明できていない可能性が高いですね。
ここで回帰モデルの評価指標について詳しく知りたい方はこちらの記事で解説しています。
【AI・機械学習】回帰モデルの性能評価および評価指標の解説|決定係数・RMSE・MAE・残差プロット
機械学習の性能評価方法の中で「回帰モデルはどうやって評価するの?」本記事ではその疑問に回答します。具体的に、決定係数、RMSE、MAE等の評価指標があり、それら特徴・利用シーンを1つずつ詳しく解説します。
【評価】残差プロットによる可視化
回帰モデルの予測結果を残差プロットとして表現します。学習データ・テストデータのサンプルともに残差の大きいプロットが目立ちますね。
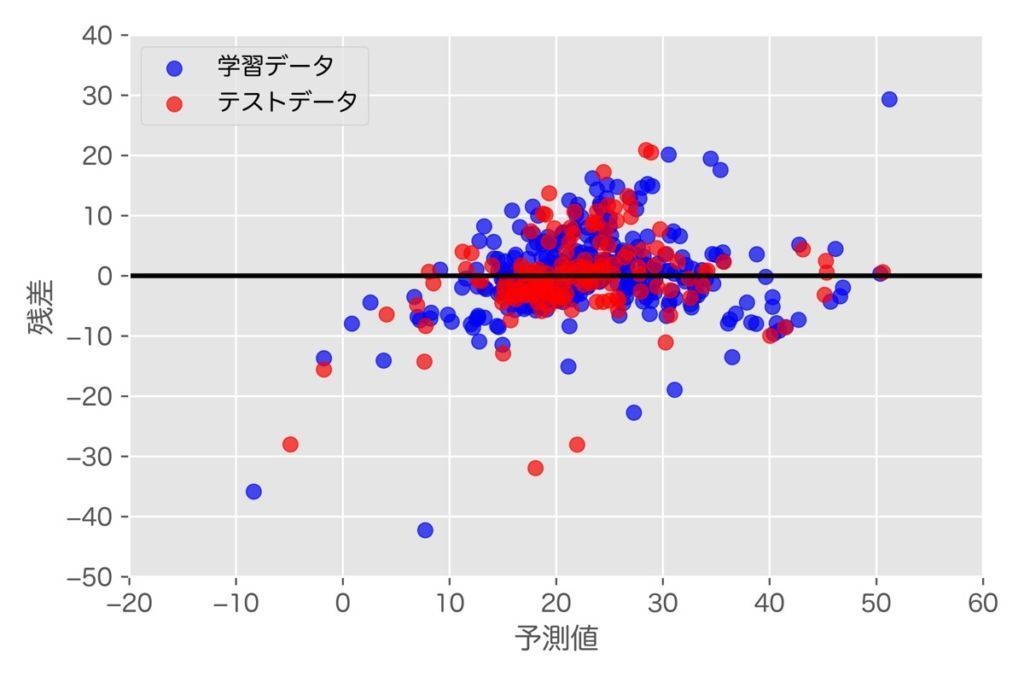
# 予測値と残差をプロット(学習データ)
plt.scatter(y_train_pred, # グラフのx値(予測値)
y_train_pred - y_train, # グラフのy値(予測値と学習値の差)
c='blue', # プロットの色
marker='o', # マーカーの種類
s=40, # マーカーサイズ
alpha=0.7, # 透明度
label='学習データ') # ラベルの文字
# 予測値と残差をプロット(テストデータ)
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='red',
marker='o',
s=40,
alpha=0.7,
label='テストデータ')
# グラフの書式設定
plt.xlabel('予測値')
plt.ylabel('残差')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-20, xmax=60, lw=2, color='black')
plt.xlim([-20, 60])
plt.ylim([-50, 40])
plt.tight_layout()
plt.show()【実践】RANSAC・ロバスト回帰モデルの作成・評価|重回帰分析
続いて、説明変数の数を増やし、モデルを作成します。
| 説明変数 | 目的変数以外の変数全て |
| 目的変数 | MEDV |
回帰モデルの学習
ロバスト回帰モデルを作成のためのコードを下記に示します。
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import RANSACRegressor
from sklearn.model_selection import train_test_split
# 変数定義
X = df.iloc[:, :-1].values # 説明変数(目的変数以外)
y = df['MEDV'].values # 目的変数(住宅価格の中央値)
# 学習・テストデータ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# ロバスト回帰モデルのインスタンス
model_ransac = RANSACRegressor(
base_estimator = LinearRegression(), # ベースモデル
min_samples=50, # ランダムに選択されたデータサンプルの最小数
residual_threshold=8.0, # 正常値として分類されるデータサンプルの最大残差(ここを大きくすると正常値として許容されるサンプル数が増える)
max_trials=200, # イテレーションの最大回数
stop_n_inliers=np.inf, # 少なくともこの数の正常値が見つかった場合は、イテレーション停止
stop_score=np.inf, # スコアが左記閾値よりも大きい場合の上位のイテレーション停止
stop_probability=0.99, # トレーニングデータの少なくとも1つの外れ値のないセットがRANSACでサンプリングされると、RANSACのイテレーションは停止
loss='absolute_loss', # 絶対誤差(absolute_loss)または二乗誤差(squared_error)が選択可能
random_state=0 # ランダムシード
)
# モデル学習
model_ransac.fit(X_train, y_train)【評価】RMSEおよび決定係数R2を用いた性能評価
RMSEと決定係数R2を用いて回帰モデルの性能評価を行います。
from sklearn.metrics import r2_score # 決定係数
from sklearn.metrics import mean_squared_error # RMSE
# 予測値(Train)
y_train_pred = model_ransac.predict(X_train)
# 予測値(Test)
y_test_pred = model_ransac.predict(X_test)
# 平均平方二乗誤差(RMSE)
print('RMSE 学習: %.2f, テスト: %.2f' % (
mean_squared_error(y_train, y_train_pred, squared=False), # 学習
mean_squared_error(y_test, y_test_pred, squared=False) # テスト
))
# 決定係数(R^2)
print('R^2 学習: %.2f, テスト: %.2f' % (
r2_score(y_train, y_train_pred), # 学習
r2_score(y_test, y_test_pred) # テスト
))
# 出力結果
# RMSE 学習: 4.90, テスト: 5.95
# R^2 学習: 0.72, テスト: 0.57説明変数の数を増やしたことで、学習データを使った決定係数R2は0.48→0.72、テストデータを使ったR2は0.39→0.57に改善されました。
性能としてはまだまだ良いとは言えませんが、今回のデータセットの場合、説明変数を複数用いたモデルの方が性能が良いと言えますね。
【評価】残差プロットによる可視化
最後にモデルの残差プロットの描画方法を下記に示します。

# 予測値と残差をプロット(学習データ)
plt.scatter(y_train_pred, # グラフのx値(予測値)
y_train_pred - y_train, # グラフのy値(予測値と学習値の差)
c='blue', # プロットの色
marker='o', # マーカーの種類
s=40, # マーカーサイズ
alpha=0.7, # 透明度
label='学習データ') # ラベルの文字
# 予測値と残差をプロット(テストデータ)
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='red',
marker='o',
s=40,
alpha=0.7,
label='テストデータ')
# グラフの書式設定
plt.xlabel('予測値')
plt.ylabel('残差')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-20, xmax=60, lw=2, color='black')
plt.xlim([-20, 60])
plt.ylim([-50, 40])
plt.tight_layout()
plt.show()【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




