こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- ロジスティック回帰分析とは何か知りたい
- ロジスティック関数の導出方法を知りたい
ロジスティック回帰分析とは
ロジスティック回帰分析とは、ある事象の発生確率Pを予測する統計学的手法になります。多変量解析や機械学習における教師あり学習の2値分類問題として取り扱われます。
ロジスティック回帰分析を利用することで、ある事象の発生確率を予測できるようになります。ここで「対象事象の発生確率の予測」とは、例えば下記のようなイメージです。
| 予測する対象事象 | 利用する目的変数(従属変数) |
|---|---|
| 子供が受験に合格する確率 | 合格=1 不合格=0 |
| 受信したメールがスパムメールである確率 | スパムメール=1 正常メール=0 |
| 患者に疾患がある確率 | 疾患あり=1 疾患なし=0 |
| 顧客が商品を購入してくれる確率 | 購入=1 見送り=0 |
| 商品の故障が発生する確率 | 故障発生=1 正常動作=0 |
ロジスティック回帰で予測する事象が取りうる値は「0または1」の2値が基本となります。
ロジスティック関数(シグモイド関数)
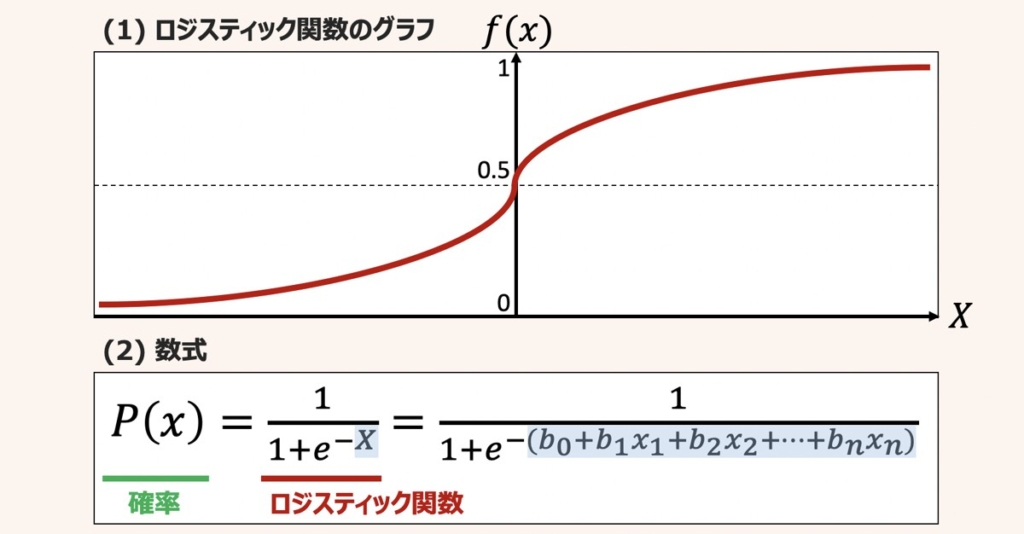
ロジスティック回帰で利用する関数をロジスティック関数(シグモイド関数)と呼び、発生確率P(x)と合わせて上図のような関係で表すことができます。
ロジスティック関数は、最小が0で最大が1となるようなS字曲線の関数です。
ロジスティック関数で得られた発生確率に対して閾値を設定し、0または1の値を出力するようにしたモデルをロジスティック回帰モデルと呼びます。閾値は発生確率P(x)=0.5として設定することが多いです。
複数の説明変数(独立変数)x1〜xnを用いて、対象事象の発生確率P(x)を求めることもできます。
ロジスティック回帰モデルの作成方法
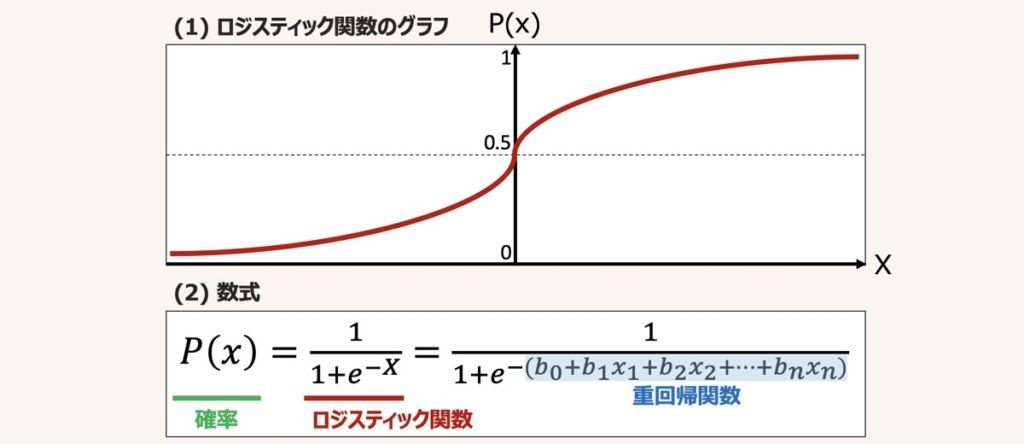
上図に示すように、ロジスティック回帰モデルは説明変数x1〜xnを入力値として受け取り、対象事象の発生確率P(x)を算出し、最終的に2値の値を返すのが特徴です。
ここで、対象事象の発生確率を精度良く予測するためのロジスティック回帰モデルを作成するには、最適なパラメータ(偏回帰係数)b0〜bnを探し出すことがポイントになります。
ロジスティック回帰モデル作成の際に採用されるパラメータ探索手法として、最尤法を用いるのが一般的です。
ロジスティック回帰では尤度関数を次のように表します。
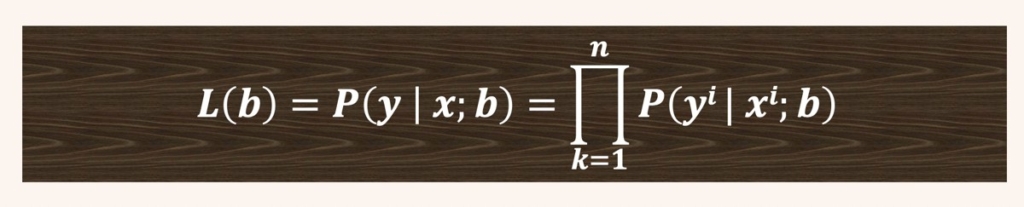
最尤法の原理や具体的な計算方法については、次の記事にて解説しています。合わせてご覧下さい。
【統計学基礎】最尤推定法とは
推定統計において、推定値算出で最もよく用いられる最尤法について詳しく解説。
ロジスティック関数の原理・導出方法
続いてロジスティック関数がそもそもどのような原理で導かれた関数であるのか、数式を追って解説します。
ロジスティック関数の計算過程で理解すべき概念として下記があります。ロジスティック関数の算出過程を追う中で併せて見ていきましょう!
- Odds(オッズ)と確率P
- Odds(オッズ)とロジット
- ロジットと確率P
- ロジスティック関数と確率P
- ロジスティック関数と説明変数
- ロジスティック回帰モデルの作成
Oddsと確率P
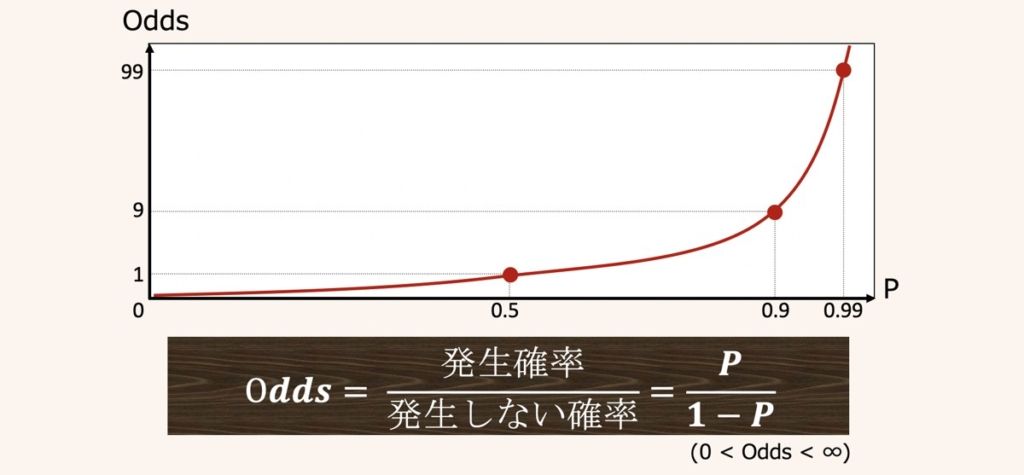
Oddsとは、ある事象の発生確率(P)/発生しない確率(1-P)として示される事象の起こりやすさを表す式です。Pは正事象の確率を示しています。
Oddsは、ギャンブルの勝率や患者に疾患がある確率など、ある事象の予測に対して古くから使われる指標です。
オッズは小さいほどその事象が発生しずらいと解釈し、1を超えると発生する確率の方が高いと解釈します。
Oddsとロジット

ロジットとは、オッズに自然対数をとった指標であり、対数Oddsとも呼ばれます。
また、上記のように確率Pから最終的にロジットを求める関数をロジット関数と呼びます。さらに、確率Pをロジットに変換することをロジット変換と呼びます。
ロジット関数は0 <= P <= 1となる入力値(確率P)を受け取り、それらを実数の全範囲の値に変換します。
ロジットと確率P
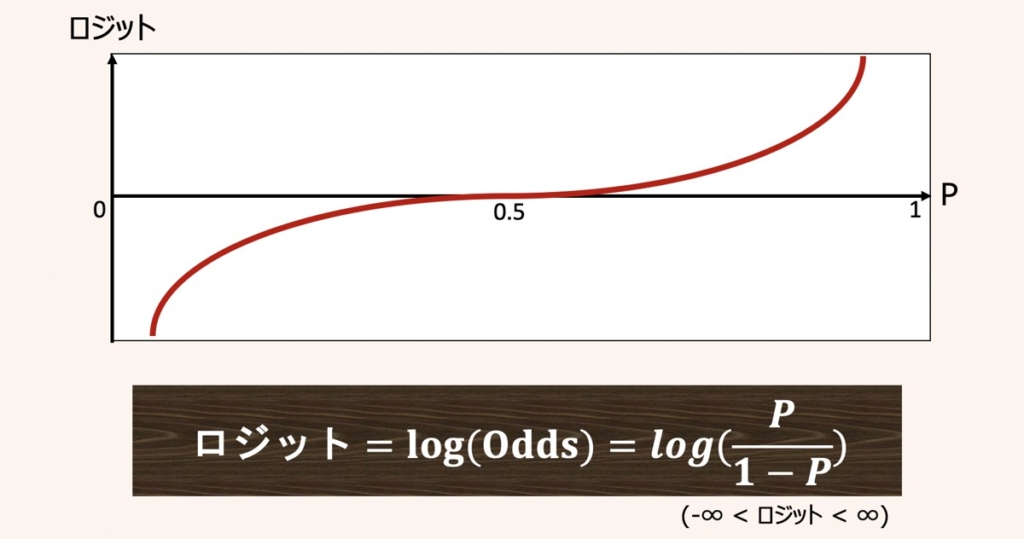
前述したロジット関数と確率Pをグラフで表すと上図のようになります。
ここまでは確率Pからロジット関数を求める方法について解説しました。統計推定や機械学習に応用する場合、ロジット関数から確率を求める関数として示す方が都合良いです。後述ではその式変形について解説します。
ロジスティック関数と確率P

ロジット関数=Xと置いた際、それぞれに対数を掛けて逆関数の形式で表すと、最終的にロジット関数から確率Pを導出するための関数を示すことができます。
上図における最終系の関数をロジスティック関数と呼びます。
ロジスティック関数と説明変数
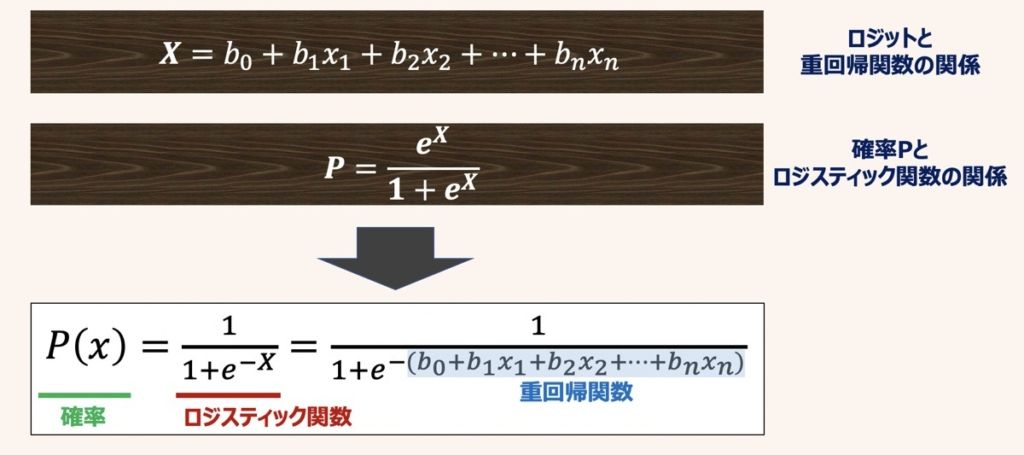
ロジットXは-∞ < X < ∞の範囲をとる変数であるため、各説明変数x1〜xnと偏回帰係b0〜bnを用いた重回帰式の関係として表すことができます。
この関係式をロジスティック関数に代入することで、上記のような説明変数から発生確率Pを算出できる関数形式へと変換できます。
ロジスティック回帰モデルの作成

最後にある事象が1(発生する) or 0(発生しない)という2値を出力するために、閾値を設定します。
上記のように、説明変数を入力した際、ロジスティック関数をもとに発生確率Pを求め、最終的に0か1を返すモデルをロジスティック回帰モデルと呼びます。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




