こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- 機械学習の教師なし学習であるk平均法(k-means法)の概要について詳しく知りたい!
- k-means法を活用したPythonプログラミング手法が知りたい!
クラスタリングとは
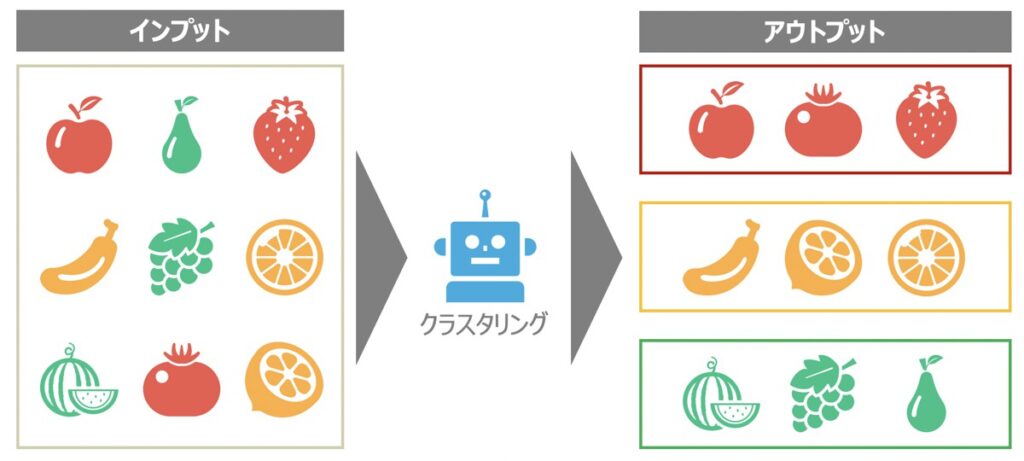
クラスタリングとは、機械学習の教師なし学習に該当するもので、類似するサンプルデータを部分集合(クラスタ)として分割することを指します。
【参考】教師なし学習

教師あり学習とは、「正解」の用意されたデータをもとに学習が行われるアルゴリズムを指します。一方、教師なし学習は「正解」データを与えずに行うアルゴリズムであり、代表的なものにクラスタリングが該当します。
教師なし学習のアルゴリズムに大量のデータを与えると、アルゴリズム自身がデータを探索し、データの構造やパターンを抽出・分類してくれるのが特徴的です。
クラスタリングの用途例
- 様々な映画・音楽・書籍を同じグループにまとめる
- 趣味・嗜好が同じ顧客別にグループ分けする
- 類似商品・類似顧客をグループ分けしてレコメンドを送る
このように、データから隠れた構造を見つけ出すことに役立つクラスタリングは、マーケティング活動におけるセグメント分析やレコメンドエンジンのアルゴリズム等に広く利用されています。
k平均法(k-means algorithm)とは
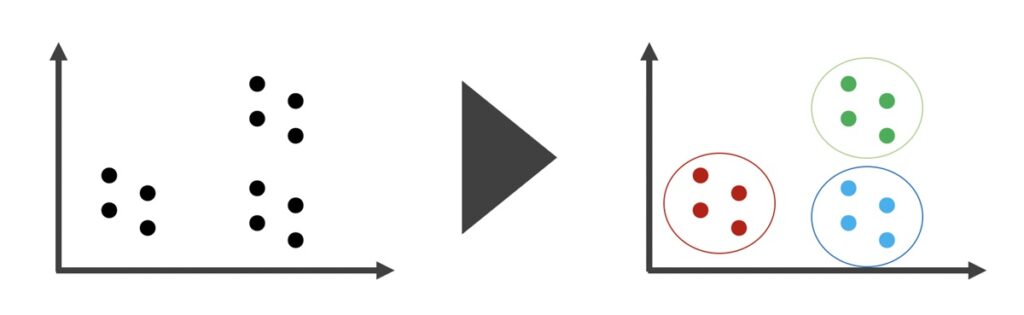
k平均法(k-means法)とは、非階層的なクラスタリングに該当する手法です。非階層的なクラスタリングとは、サンプルデータをいくつのクラスターに分けるか事前に指定し、指定したクラスター数に基づきサンプルを分割するという方法です。上図の場合、3つのクラスターに分割したと言えます。
k平均法のメリット
k平均法は、実装が容易であり他のクラスタリング手法と比較しても計算効率が優れている、データ容量の大小問わず広く利用できるというメリットがあります。
k平均法のデメリット
階層的クラスタリングと異なり、最適なクラスター数を導き出すにはクラスター数を人為的に探索・決定する必要があるのが課題です。
階層クラスタリング vs k平均法
データ容量が比較的小さいサンプルには階層クラスタリングが採用され、ビッグデータなど容量が大きいサンプルにはk平均法のような非階層的クラスタリングが採用される傾向があります。
階層クラスタリングについて詳しく知りたい方はこちらの記事をご覧下さい。
【AI・機械学習】階層的クラスタリングのモデル・樹形図(デンドログラム)作成・クラスター分析|教師なし学習
機械学習の教師なし学習であるクラスタリング分析実施にあたり、本記事では「階層的クラスタリングの概要とそのプログラミング手法を知りたい」という要望にお答えします。記事前半は階層的クラスタリングの概要解説、後半はプログラミング手法解説という構成です。
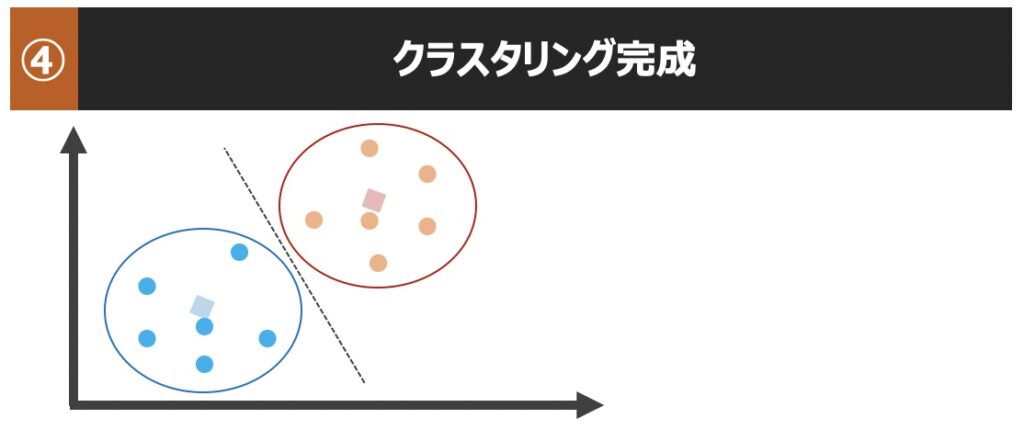
【k-means原理】k平均によるクラスタリング実行までの流れ
k平均法に基づくクラスタリングでは、具体的にどのようにサンプルが分割され、クラスターが生成されるのでしょうか?以下クラスター生成までの流れを直感的に理解してみましょう!
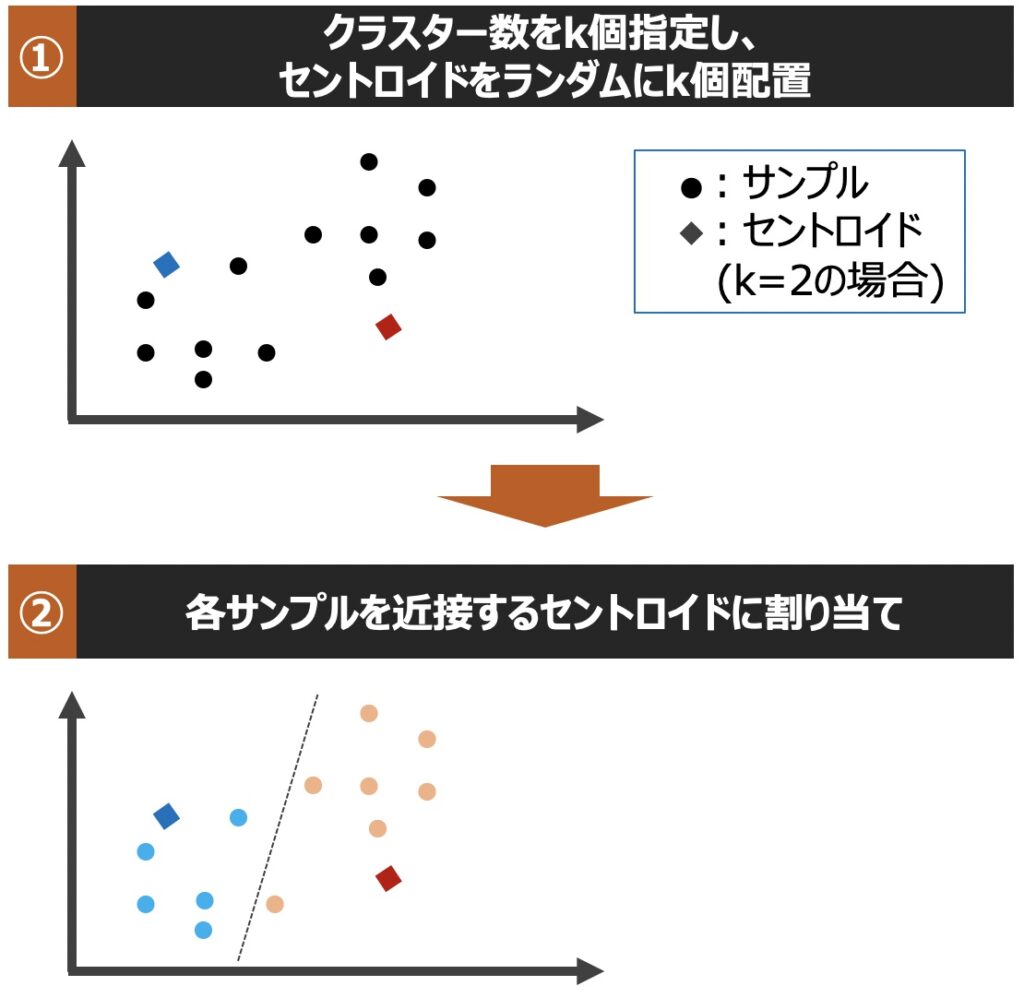
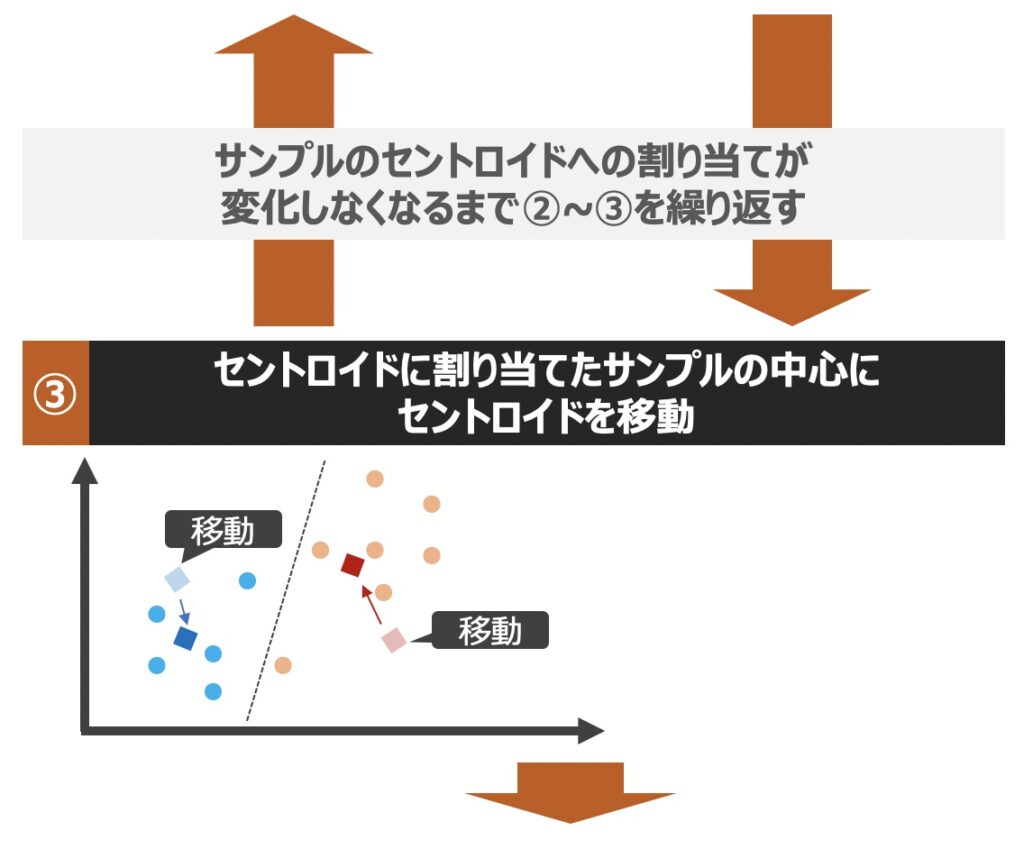
| 用語 | 意味 |
|---|---|
| セントロイド (Centroid) | サンプルデータが連続的な場合において、類似する「中心点」を指す |
| メドイド (Medoid) | サンプルデータがカテゴリー値の場合において、最も「代表的」または「頻度が高い」点を指す |
クラスタリングの評価指標
機械学習における教師なし学習は、教師あり学習と異なり、明確な答えが用意されていないという課題があります。そのため、クラスタリング性能を定量的に評価するには、何か指標を用いて地道に比較することが大切になります。
エルボー法
最適なクラスタ数を求める方法としては、「エルボー法」がよく用いられます。エルボー法とは、クラスタ内誤差平均和(SSE)という指標に基づき、最適なクラスタ数を導出する方法です。SSEとは、各クラスタのセントロイドから各サンプルまでの距離の総和であり、下記のような規則性を有します。
エルボー法を用いた最適なクラスター数の推定
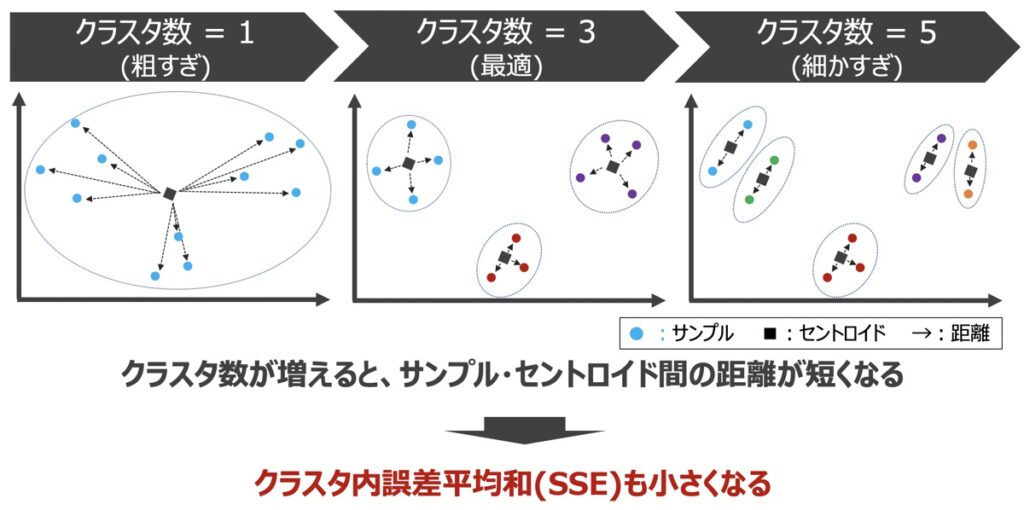
上記をグラフに表すと下記のようなイメージになります。
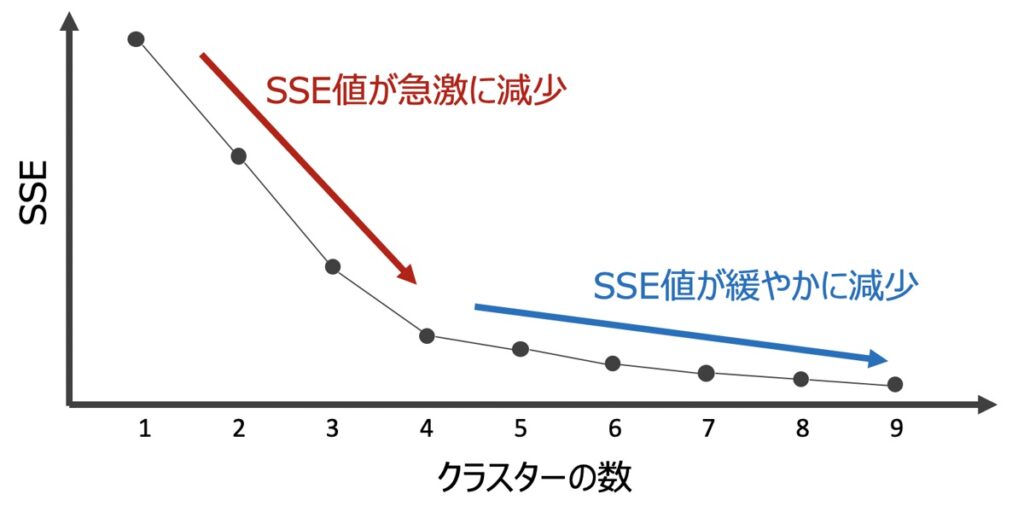
上記グラフを用いたエルボー法では、SSE値が急激に減少している部分において、SSE値が最も小さい点が最適なクラスター数であると判断します。(上図例だとクラスター数=4が最適)
シルエット図
クラスタリングの性能を評価する他の指標として、シルエット分析があります。シルエット分析とは下記の基準に基づきクラスタリング性能を評価するもので、k平均法意外のクラスタリングアルゴリズムにも適用できる分析手法です。
- クラスタ内のサンプルが密にグループ化されている(凝集度が高い)ほど良い
- 異なるクラスタは距離が離れているほど良い
シルエット係数
クラスタリング性能は、シルエット係数(silhouette coefficient)を用いて評価されます。
- :凝集度(同一クラスタのサンプル(i)と他の全サンプルとの平均距離)
- :乖離度(サンプル(i)から最も近くにあるクラスタ内全サンプルとの平均距離)
- :シルエット係数
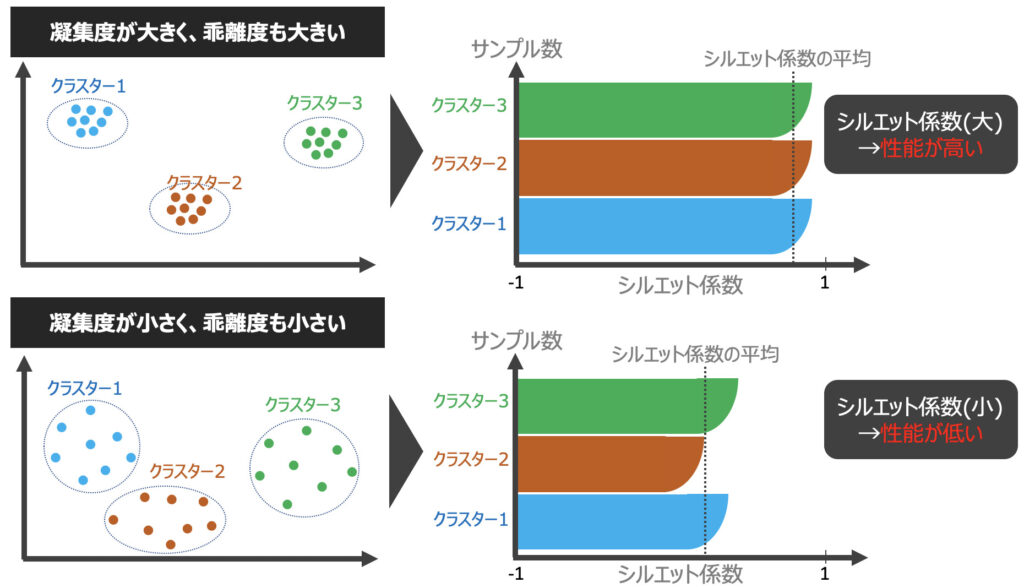
シルエット係数は[-1:1]の範囲を取り、シルエット係数が1に近づくほどクラスタリング性能が良いと判断できます。また、下記グラフのように可視化することで性能の優劣が判断しやすくなります。
シルエット図を用いたクラスタリング性能の評価
【Python】k平均法(k-means)によるクラスタリングモデル構築
k平均法を用いたクラスタリングモデルを構築するにあたり、ここからは実際にpythonによるプログラミングを実践します。
クラスタリングモデル構築手順
モデル構築は下記の手順で実施します。
- データの準備・理解
- エルボー法を用いた最適なクラスター数の推定
- クラスタリングモデル作成
- シルエット図を用いたモデル性能評価
データの準備・理解
本記事では「顧客属性別の居住マンション価格に関するデータセット」を用いており、顧客の年収とマンションにかかる費用で顧客をグループ分けすることします。
サンプルデータ
コード
import pandas as pd
df = pd.read_csv("sample_data.csv")
# クラスタリング軸(年収 vs マンション費用)
X = df.iloc[:, [3, 4]].values
# 出力
print(df.tail())出力結果
表:sample_data.csvのデータ例
| 性別 | 年齢 | 職業 | 年収[万円] | マンション費用[万/月] |
|---|---|---|---|---|
| 男 | 32 | 商社 | 700 | 12 |
| 女 | 26 | 公務員 | 350 | 4 |
エルボー法を用いた最適なクラスター数の指定
エルボー法を用いて最適なクラスター数を推察します。下記のように記述しましょう。
コード
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = 'Hiragino Maru Gothic Pro'
# クラスタリング軸の指定( 年収 vs マンション費用 )
X = df.iloc[:, [3, 4]].values
# エルボー法
max_cluster = 15
SSE = []
for i in range(1,max_cluster):
#インスタンス
kmeans = KMeans(n_clusters = i, # クラスタの個数
init = 'k-means++', # k平均++法によりクラスタ中心を選択
n_init = 5, # 異なるセントロイドの初期値を用いたk平均法アルゴリズム実行回数
max_iter = 350, # k平均法アルゴリズム内部の最大イテレーション(サイクル繰り返し)回数
tol = 1e-04, # 収束と判定できる相対的許容誤差
random_state = 42 # セントロイド初期化に際して、用いる乱数生成器の設定
)
# 演算
kmeans.fit(X)
# wcss値に変換&リスト格納
SSE.append(kmeans.inertia_)
# 可視化
plt.plot(range(1,max_cluster), SSE)
plt.title('エルボー法による最適なクラスター数の調査')
plt.xlabel('クラスター数[個]')
plt.ylabel('SSE')
plt.show()出力グラフ
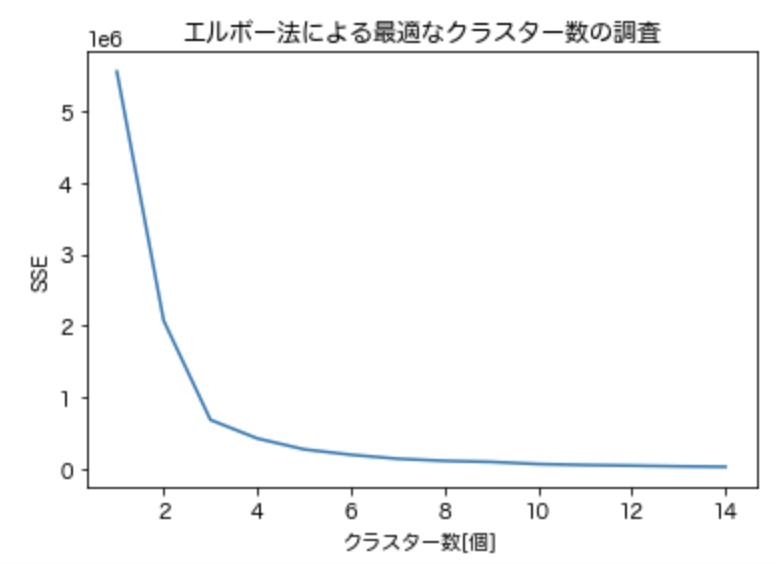
上記の場合、クラスター数が3に至るまでSSEが急激に減少し、それ以降は緩やかに減少していることが分かります。従って、今回活用しているデータにおいて最適なクラスター数は3であると推察できます。
クラスタリングモデル作成
エルボー法で算出したクラスターの個数をもとに、k-meansアルゴリズムに基づくクラスタリングモデルを作成します。下記のように記述してみましょう。
コード
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = 'Hiragino Maru Gothic Pro'
# ================================================
# モデル作成
# ================================================
# クラスタリング軸を指定( 年収 vs マンション費用 )
X = df.iloc[:, [3, 4]].values
# k-meansインスタンス
kmeans = KMeans(n_clusters = 3, # クラスタの個数
init = 'k-means++', # k平均++法によりクラスタ中心を選択
n_init = 5, # 異なるセントロイドの初期値を用いたk平均法アルゴリズム実行回数
max_iter = 350, # k平均法アルゴリズム内部の最大サイクル繰り返し回数
tol = 1e-04, # 収束判定する相対的許容誤差
random_state = 42 # セントロイド初期化に際して、用いる乱数シードを設定
)
# 演算
y_kmeans = kmeans.fit_predict(X)
# ================================================
# 可視化
# ================================================
# 配列情報
cluster_labels = np.unique(y_kmeans) # 一意なクラスター要素
n_clusters = cluster_labels.shape[0] # 配列の長さ
# 各クラスターの可視化
for i in range(len(cluster_labels)):
color = cm.jet(float(i) / n_clusters)
plt.scatter(X[y_kmeans == i, 0],
X[y_kmeans == i, 1],
s = 20,
color = color,
label = f'Cluster{i}'
)
# セントロイドの可視化
plt.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
s = 80,
color = 'red',
label = 'Centroids'
)
plt.title('顧客属性クラスター')
plt.xlabel('年収[万円]')
plt.ylabel('マンション費用[万円/月]')
plt.legend()
plt.show()出力グラフ
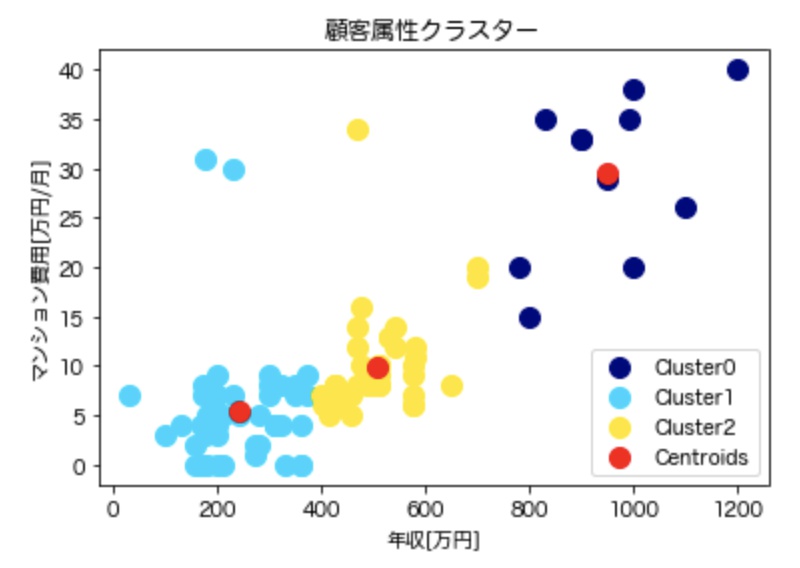
k-means法ひな型コード
下記条件を有するインスタンスに基づき、k-meansモデルを構築しています。
from sklearn.cluster import KMeans
# k-meansインスタンス
kmeans = KMeans(n_clusters = 3, # クラスタの個数
init = 'k-means++', # k平均++法によりクラスタ中心を選択
n_init = 5, # 異なるセントロイドの初期値を用いたk平均法アルゴリズム実行回数
max_iter = 350, # k平均法アルゴリズム内部の最大サイクル繰り返し回数
tol = 1e-04, # 収束判定する相対的許容誤差
random_state = 42 # セントロイド初期化に際して、用いる乱数シードを設定
) k-means法に用いる引数一覧
sklearn.cluster.KMeansインスタンスの引数には下記を与えることができます。
| 引数名 | 概要 | デフォルト |
|---|---|---|
| n_clusters | クラスタの個数 | 8 |
| init | 初期化方法(k-means++, random, ndarray) | k-means++ |
| n_init | 異なるセントロイドの初期値を用いたk平均法アルゴリズム実行回数 | 10 |
| max_iter | k平均法アルゴリズム内部の最大サイクル繰り返し回数 | 300 |
| tol | 収束判定する相対的許容誤差 | 0.0001 |
| precompute_distance | 距離(バラツキ)のを事前計算するか(auto,True,False) | auto |
| verbose | 1を指定し分析詳細を表示(1,0) | 0 |
| random_state | セントロイド初期化に際して、用いる乱数シードを設定 | 0 |
インスタンスのパラメーターは下記のように確認することが可能です。
kmeans.get_params
# 出力結果
# <bound method BaseEstimator.get_params of KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=350,
# n_clusters=3, n_init=5, n_jobs=None, precompute_distances='auto',
# random_state=42, tol=0.0001, verbose=0)>シルエット図を用いたモデル性能評価
最後にシルエット分析を用いてクラスタリングモデルの性能評価を実施します。下記のように記述しましょう。
コード
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
# 配列情報
cluster_labels = np.unique(y_kmeans) # 一意なクラスター要素
n_clusters = cluster_labels.shape[0] # 配列の長さ
# ================================================
# シルエット係数
# ================================================
# シルエット係数の計算
silhouette = silhouette_samples(X,y_kmeans, metric="euclidean")
axis_y_btm, axis_y_up = 0, 0
y_list = []
# シルエット係数・グラフデータ計算
for i,label in enumerate(cluster_labels):
wd_silhouette = silhouette[y_kmeans == label]
wd_silhouette.sort()
axis_y_up += len(wd_silhouette)
color = cm.jet(float(i) / n_clusters)
# 水平棒グラフ
plt.barh(
range(axis_y_btm, axis_y_up), # 底辺の範囲
wd_silhouette, # 棒の幅
height = 1.0, # 棒の高さ
edgecolor = "none", # 棒端の色
color = color, # 棒の色
)
# クラスラベルの表示位置追加
y_list.append((axis_y_btm + axis_y_up) /2)
# 底辺の値に棒の幅を追加
axis_y_btm += len(wd_silhouette)
# シルエット係数の平均値
silhouette_mean = np.mean(silhouette)
# ================================================
# 可視化
# ================================================
plt.axvline(silhouette_mean, color="r", linestyle="--")
plt.yticks(y_list, cluster_labels+1)
plt.ylabel("クラスター")
plt.xlabel("シルエット係数")
plt.tight_layout()
plt.show()出力グラフ
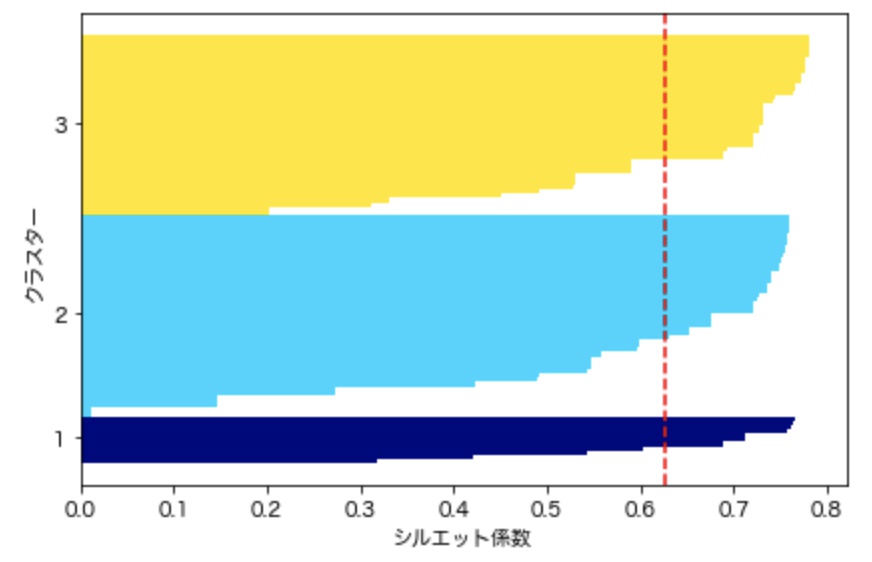
シルエット係数が1であれば性能が良いクラスタリングと言えますが、今回の例では係数が0.6~0.7付近であることから、あまり性能が良いとは言えません。このような結果が出た場合、クラスタリング数を変更等行うことで性能比較を繰り返し、最適なモデルを探求するのが良いでしょう。
【参考】クラスター分析の学習におすすめの教材
最後までご覧いただきありがとうございました。クラスタリングは教師なし学習の代表的手法であり、データにある隠れた規則性を見出すのに非常に有効な手法です。
以下本日の学習ポイントまとめです。
最後に、Pythonを用いたクラスター分析についてもっと学習したい方向けにおすすめ教材を紹介します。興味のある方は是非ご覧下さい。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら






