こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- 機械学習の教師あり学習に該当するk近傍法(KNN)について詳しく知りたい
- Pythonとscikit-learnを用いてKNNモデルを実装・評価する方法が知りたい
【機械学習】k近傍法(KNN)とは
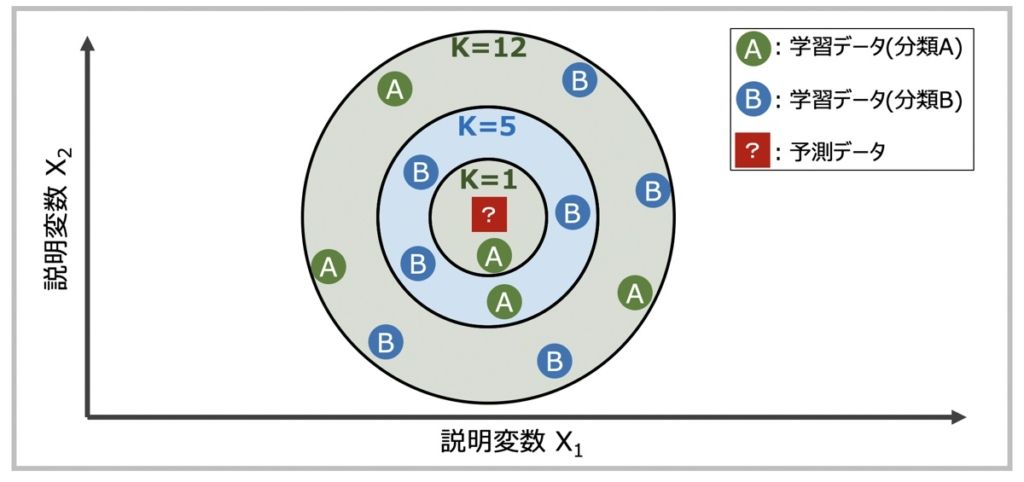
k近傍法(K-Nearest Neighbor Algorithm)とは、機械学習の教師あり分類アルゴリズムの1つです。KNNによる分類の特徴は、未知のデータに着目した際、そのデータの近隣情報に基づき、分類結果を予測することです。
K近傍法による未知のデータ分類イメージ

K近傍法では、データ空間のユークリッド距離(またはマンハッタン距離)で最も近い点を探索する「最近傍探索問題」に基づき分類が実行されます。
例として上図を見てみましょう。ここでのKとは、未知のデータからの最近距離順位を示すハイパーパラメータです。未知のデータ[?]に対して距離が近い順にK個の学習データを指定し、多数決で分類を決定します。実際の機械学習モデル構築の際は、このKの値を何にするかによって精度が大きく変わるので考慮が必要です。
【Python】scikit-learnでk近傍法(KNN)の機械学習モデルを構築
それでは実際にPythonのScikit-learnライブラリを用いてKNNのモデルを構築していきましょう!具体的に下記の手順でプログラムを構築していきます。
- データセットの説明
- データの準備
- knnモデル学習
- モデル性能評価とハイパーパラメータ(k)のチューニング
データセットの説明

データセットには、機械学習のサンプルデータとして有名なIris(アヤメ)データセットを活用します。3種類のアヤメ(Iris Setosa, Iris Versicolor, Iris Virginica)があり、それぞれ50サンプルずつ(合計150サンプル)用意されているデータです。このアヤメの名前を目的変数として利用します。また、説明変数にはアヤメの計測値である萼片(sepals)と花びら(petals)の長さと幅の4つを利用します。
データの準備
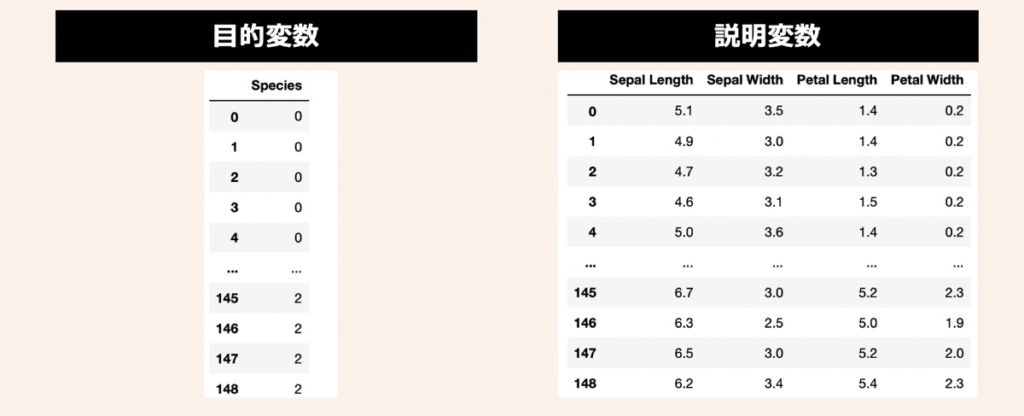
まず、前述したアヤメのデータセットを準備します。上記目的変数と説明変数をPandas形式で取り扱うために、下記のコードを実行してみましょう。
"""
①データセットの準備(Sckit-learnで提供されているアヤメのデータを利用)
"""
import numpy as np
import pandas as pd
from sklearn import datasets
# データロード
iris = datasets.load_iris()
# 説明変数
X = iris.data
X = pd.DataFrame(X, columns=["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"])
# 目的変数
Y = iris.target
Y = iris_target = pd.DataFrame(Y, columns = ["Species"])後述では変数(X)を説明変数の集合体、変数(Y)を目的変数として利用していきます。今回データ加工やクレンジング、特徴量エンジニアリング等の前処理工程は割愛します。
knnモデル学習
knnのインスタンスを作成し、モデル学習を行います。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
# 学習データおよびテストデータ分割
X_train,X_test,Y_train,Y_test = train_test_split(X,Y, test_size=0.3, shuffle=True, random_state=3)
# インスタンス
knn = KNeighborsClassifier(n_neighbors=3)
# モデル学習
knn.fit(X_train,Y_train)ここでknnのインスタンス作成において、前述で言及した最近距離順位Kとは「n_neighbors」を指します。今回はデフォルトで「3」と指定してみました。
モデル性能評価とハイパーパラメータ(k)のチューニング
作成したモデルの性能評価を行ってみましょう!
【モデル評価】正解率・適合率・再現率の評価
正解率・適合率・再現率を用いて性能評価を行います。下記のように記述してみましょう。
# 性能評価
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
# 推論
Y_pred = knn.predict(X_test)
# 性能評価
print("正解率: " + str(round(accuracy_score(Y_test,Y_pred),3)))
print("適合率: " + str(round(precision_score(Y_test,Y_pred, average="macro"),3)))
print("再現率: " + str(round(recall_score(Y_test,Y_pred, average="macro"),3)))
# 出力結果
# 正解率: 0.956
# 適合率: 0.958
# 再現率: 0.952正解率は約96%という結果が得られました。適合率・再現率においても、ともに高い結果が得られました。
【グラフ可視化】kを変化させた時のモデル性能の推移
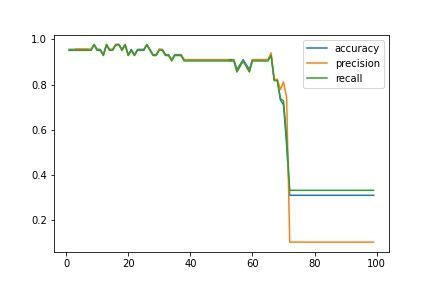
最後にモデル精度向上を目指してハイパーパラメータのチューニングを行い、最適なKの値を探索してみましょう!上図のように縦軸に正解率(Accuracy)・適合率(Precision)・再現率(Recall)、横軸にKの値をプロットできるプログラムを記述します。
# kの値を1~90まで変化させた際の正解率・適合率・再現率を観察
import matplotlib.pyplot as plt
accuracy = []
precision = []
recall = []
k_range = range(1,100)
for k in k_range:
# モデルインスタンス作成
knn = KNeighborsClassifier(n_neighbors=k)
# モデル学習
knn.fit(X_train,Y_train)
# 性能評価
Y_pred = knn.predict(X_test)
accuracy.append(round(accuracy_score(Y_test,Y_pred),3))
precision.append(round(precision_score(Y_test,Y_pred, average="macro"),3))
recall.append(round(recall_score(Y_test,Y_pred, average="macro"),3))
# グラフプロット
plt.plot(k_range, accuracy, label="accuracy")
plt.plot(k_range, precision, label="precision")
plt.plot(k_range, recall, label="recall")
plt.legend(loc="best")
plt.show()
# 結果出力
max_accuracy = max(accuracy)
index = accuracy.index(max_accuracy)
best_k_range = k_range[index]
print("「k="+str(best_k_range)+"」の時、正解率は最大値「"+str(max_accuracy)+"」をとる")
# 出力結果
# 「k=9」の時、正解率は最大値「0.978」をとるグラフの結果を見ると、今回の例ではK(n_neighbors)=9の時に最も正解率の高い機械学習モデルが構築できることが分かりました。このように、精度が最大となるパラメータKを探索することでKNNを用いたモデルは作成することができます。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




