【統計学基礎】カイ二乗分布｜Pythonでの描画方法も解説

2022年5月19日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

こんな方におすすめ

カイ二乗分布の概要を詳しく理解したい
Pythonでカイ二乗分布を描画する方法を知りたい

カイ二乗分布とは｜χ²分布

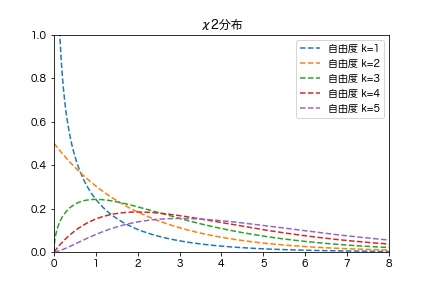
母集団が正規分布に従っているとき、標本の偏差平方和が従う確率分布をカイ二乗分布（χ²分布）といいます。

χ²分布（chi-squared distribution)

独立な確率変数Y₁, Y₂, Y₃, Y₄, ・・・, Y_nがそれぞれ標準正規分布N(0, 1)に従う場合、確率変数Xを次のように置く。

X = Y₁¹ + Y₂² + Y₃³ + Y₄4+ Y_k²

Xが従う確率分布を自由度kのχ²分布といい、χ²(k)として表す。

自由度が1のとき、カイ二乗分布は標準正規分布に従う確率変数を二乗したものに等しい。

χ²(1) = Y₁²

推測統計では、正規分布に従う母集団の平均や分散を標本の平均や分散をもとに推測します。ここで、標本平均や分散をそのまま母集団の平均や分散の予測値として使うことも可能ですが、標本の平均や分散を確率分布として捉えることで、より精細に母集団の平均や分散の確らしさを検証できるようになります。ここで用いる代表的な分布としてカイ二乗分布、t分布、F分布があります。

【参考】推測統計で用いる代表的な分布

母集団が正規分布に従うものとした場合、次のような標本の確率分布が得られます。

カイ二乗分布	標本の偏差平方和が従う確率分布
t分布	標本平均を標本の分散で標準化した値が従う確率分布
F分布	母分散が等しい2つの標本の分散比が従う確率分布

本記事ではカイ二乗分布の性質についてより詳しく解説していきます。

【参考】Python×統計学の学習におすすめな教材

「データ分析する上で統計学の基礎を学びたい」「Pythonで動かしながら統計解析を学びたい」方向けに以下の教材をおすすめします。

データ分析で必須の統計学基礎を学びたい方向け

Pythonと併用して統計解析を学びたい方向け

Pythonで実際に動かしながら学習することで、プログラミングに加え、統計学の応用も合わせた深い知識習得が期待できます。

カイ二乗分布の性質

カイ二乗分布の性質について以下言及します。

カイ二乗分布の確率密度関数

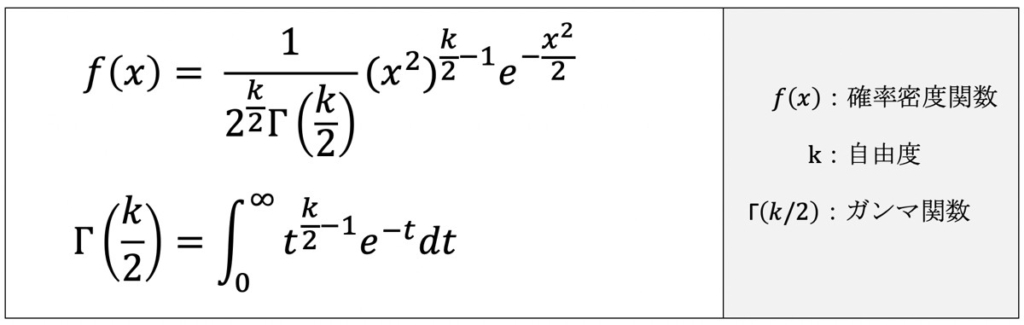
自由度kのカイ二乗分布の確率密度関数f(x)は上記の式で表せます。

カイ二乗分布の期待値

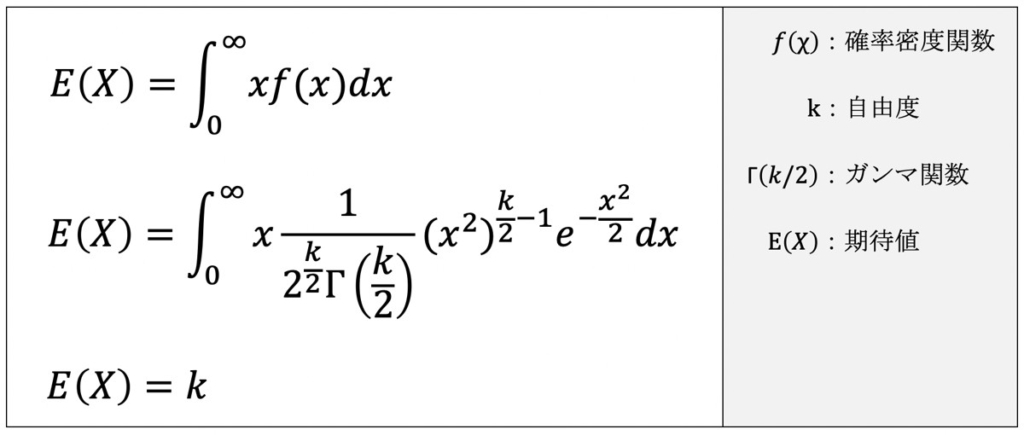
確率変数Xが自由度kのカイ二乗分布に従う場合、Xの期待値E(X)は上記のように示されます。

カイ二乗分布の分散

確率変数Xが自由度kのカイ二乗分布に従う場合、Xの分散V(X)は上記のように示されます。

カイ二乗分布の再生性

2つの確率変数X₁, X₂がそれぞれ独立に、自由度k₁、k₂のカイ二乗分布χ²(k₁)、χ²(k₂)に従うとき、確率変数の和X₁+ X₂もカイ二乗分布χ²(k₁+k₂)に従い、その自由度はk₁+k₂として示されます。

正規分布に従う母集団からの無作為標本とカイ二乗分布

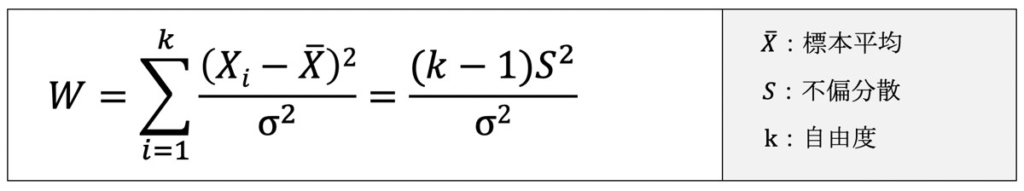
正規分布N(μ, σ²)に従う母集団から無作為抽出されたX₁, X₂, X_kについて、互いに独立のXが正規分布に従う場合、Wは自由度k-1のカイ二乗分布に従います。

【Python】カイ二乗分布のグラフ

カイ二乗分布のグラフは自由度別に上記のように表されます。自由度によって形状が異なるのが特徴です。カイ二乗分布の自由度は、足される独立な標準正規分布の個数によってグラフの形状が決まります。

Pythonを用いてカイ二乗分布を描画する方法について解説します。次のようなコードを実行してみましょう。

# カイ二乗分布算出
from scipy.stats import chi2
import numpy as np

# グラフ
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams["font.family"]     = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"
# %matplotlib inline


"""
****************************************
カイ二乗分布
****************************************
"""
# X
x = np.linspace(0, 8, 10000)

# 自由度 k=1〜5
k_deg = [1, 2, 3, 4, 5]

# 自由度 n=1〜5 までのグラフを描画
for i in k_deg:
    plt.plot(x, chi2.pdf(x, i), linestyle='--', label='自由度 k={}'.format(i))

"""
****************************************
グラフの書式設定
****************************************
"""
plt.title("χ2分布")   # タイトル
plt.xlim(0, 8)       # X軸範囲
plt.ylim(0, 1)       # Y軸範囲
plt.legend()         # 凡例
plt.show()

カイ二乗分布の確率密度関数は、scipy.stats.chi2.pdf()メソッドに確率変数Xの値と自由度kを与えることで、簡単に算出することができます。