【統計学基礎】t分布とは｜Pythonでの描画方法も解説

2022年5月18日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

こんな方におすすめ

t分布について詳しく理解したい
Pythonでt分布を描画する方法が知りたい

t分布とは

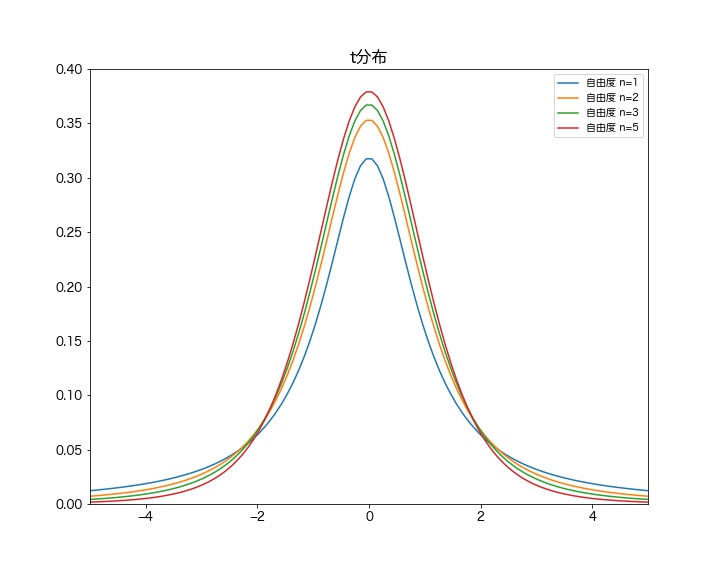
母集団が正規分布に従っているとき、標本平均を標本の分散で標準化した値が従う確率分布をt分布（t-distribition）と呼びます。t分布は自由度が増加すると、標準正規分布のグラフに近づきます。

t分布の公式

独立な確率変数Y, Zがあり、確率変数Yが正規分布N(0,1)、Zが自由度nのカイ二乗分布に従う場合、確率変数Xは次のように表されます。

この時Xが従う確率分布を自由度nのt分布と呼び、t(n)として表されます。

カイ二乗分布の公式は平方和であるため、分散を想像しますね。上記に示したt分布の公式は、分母にルートがあるため標準偏差を連想させ、その中にカイ二乗分布があるため、t分布の公式は標準化している式であることが分かります。

ここでカイ二乗分布について詳しく知りたい方はこちらの記事をご覧下さい。

【参考】Python×統計学の学習におすすめな教材

「データ分析する上で統計学の基礎を学びたい」「Pythonで動かしながら統計解析を学びたい」方向けに以下の教材をおすすめします。

データ分析で必須の統計学基礎を学びたい方向け

Pythonと併用して統計解析を学びたい方向け

Pythonで実際に動かしながら学習することで、プログラミングに加え、統計学の応用も合わせた深い知識習得が期待できます。

t分布の特徴

t分布の性質について以下言及します。

t値｜スチューデントのt分布

母平均μ、母分散σ²の正規分布N(μ, σ²)に従う母集団から抽出したサンプルサイズnの標本をX₁, X₂, ・・・, X_nとする場合、以下のように示された確率変数tは、標準正規分布N(0,1)に従います。

ここで母分散σ²が分からない場合、上記公式は利用できません。

そこで母分散σ²の代わりに、n→∞の時にσ²に収束する不偏分散s²を用い、上記の式を次のように変換します。

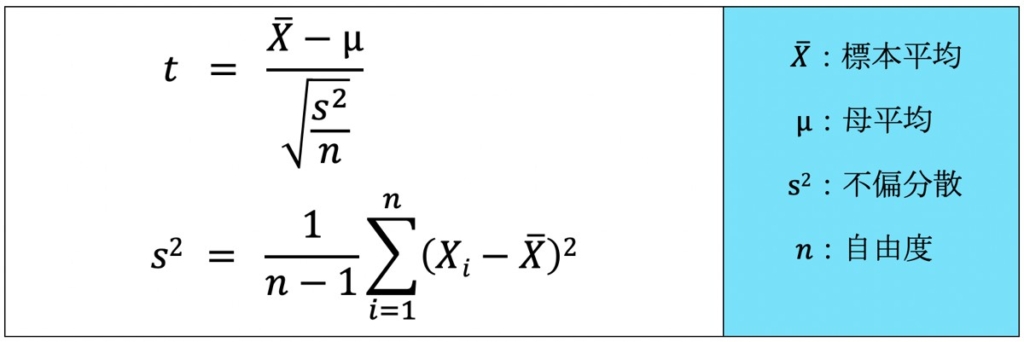
上記tは、自由度(n-1)のt分布に従います。このように、母分散σ²を不偏分散s²に置き換えた統計量に変換することをスチューデント化と呼びます。

通常母平均の区間推定では、上式いづれかに基づくt分布を用います。一方で、母平均が未知の値である場合、母分散だけ既知の値である場合はほとんどありません。ゆえに、不偏分散に置き換えた上式を用いて、区間推定を行うのが一般的です。

t分布の確率密度関数

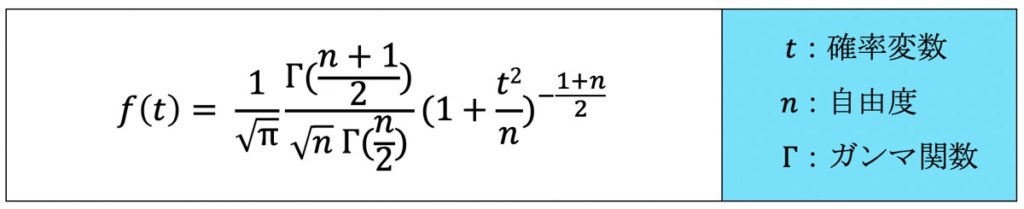
前述の統計量t値が従うt分布において、その確率密度関数f(t)は上式のように表されます。

t分布の期待値

確率変数Xが自由度nのt分布に従う場合、Xの期待値E(X)は上記のように示されます。

t分布の分散

確率変数Xが自由度nのt分布に従う場合、Xの分散V(X)は上記のように示されます。

【Python】t分布のグラフ描画方法

自由度nのt分布t(n)をPythonで描画する方法について解説します。以下のコードを実行してみましょう。

# t分布の計算
from scipy.stats import t
import numpy as np

# グラフ可視化
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams["font.family"]     = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"



"""
****************************************
t分布
****************************************
"""
# グラフ設定
fig,ax = plt.subplots(1,1, figsize=(10,8))

# X軸
X = np.linspace(-5,5,100)

# 自由度 n = 1〜5までを用意
n_deg = [1,2,3,5]

# 自由度 n=1〜5までのグラフを描画
for i in n_deg:
    ax.plot(X, t(i).pdf(X), linestyle='-', label="自由度 n={}".format(i))


"""
****************************************
グラフ書式設定
****************************************
"""    
plt.xlim(-5, 5)              # X軸範囲
plt.ylim(0, 0.4)             # Y軸範囲
plt.xticks(fontsize= 12)     # X軸フォントサイズ
plt.yticks(fontsize= 12)     # Y軸フォントサイズ
plt.title("t分布", size=16)   # タイトル
plt.legend()                 # 凡例
plt.show()

t(n)の確率密度関数は、scipy.stats.t(n).pdf()メソッドを用いて導出できます。