仮説検定とは｜図解ありの統計学基礎学習入門

2022年5月26日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

こんな方におすすめ

仮説検定の概要を詳しく理解したい方向けに「仮説検定の概要・手順」「図解と交えた仮説検定の事例」をそれぞれ詳しく解説します。

仮説検定とは

仮説検定とは、ある仮説が正しいと言ってよいか、統計学的、確率論的に判断・検証する手法です。

小学2年生陸上競技のソフトボール投げで、遠投距離が24mの男子生徒がいたとします。あなたは、その人のことを小学5年生の生徒であると考えたとします。小学2年生の男子生徒のソフトボール投げ平均遠投距離は11mです。24mはそれに比べてかけ離れた記録であるため、小学2年生の生徒ではないと思ったのです。これが検定の原理です。

すなわち、確率が小さいことが起こったとき（男子生徒のソフトボール投げが24m）には、前提となる仮説（小学2年生の男子生徒である）を破棄し、前提を否定する仮説（小学2年生の男子生徒ではない）を得るということです。

仮説検定の実施手順

仮説検定は次のような手順で実行されます。

帰無仮説、対立仮説を立てる
有意水準pを設定する
帰無仮説のもとで、現実に起こったことの確率（検定統計量）を求める
検定統計量の確率分布を明らかにする
検定統計量が有意水準p以内であるか確認する
帰無仮説を棄却または採択する

帰無仮説・対立仮説を立てる

検定を行うために設定する仮説を帰無仮説と呼びます。加えて対立仮説という帰無仮説に対する反対の仮説を設定します。

帰無仮説（H₀）	・検定の初段階で立てる仮説・帰無仮説をもとに検定を実施し結論を導く
対立仮説（H₁)	・帰無仮説に対する反対の仮説・本来証明したい仮説を対立仮説として立てる

ソフトボール投げの問題では「男子生徒が小学2年生であるか」を検証するために、以下の仮説を立てています。

ソフトボール投げで24mを記録した男子生徒は「小学2年生の生徒である」
ソフトボール投げで24mを記録した男子生徒は「小学2年生の生徒ではない」

有意水準（p値）を設定する

有意水準とは帰無仮説が間違っていると判断するための基準となる確率です。

例えば、有意水準0.05と設定した場合、5%以下の確率で生じる帰無仮説の事象は、めったに起こらない事象であると判断します。

現実に起こった確率が、有意確率として定めた値（p値）より大きい場合は帰無仮説を採択し、小さい場合は帰無仮説を棄却して対立仮説を採択します。

検定統計量(test statistic)

仮説検定のために、標本データから一定のルールに従って算出された統計量を検定統計量と呼びます。

例えば、母集団の母数（平均値や標準偏差など）を検定するために、母集団から抽出した標本の値を確率変数X₁, X₂,・・・X_nとみなしたとします。さらに、母数を検定するために、X₁、X₂、・・・X_nから作った確率変数T（X₁、X₂、・・・、X_n）を作ったとします。がここでいう確率変数Tが検定統計量となります。母数の検定には、検定統計量Tが従う分布を用いて、標本の実現値（帰無仮説の事象）が起こる確率を計算します。

なお、検定統計量の作成方法は、母集団の分布や検定する母数により異なっており、この点は本記事後半で言及します。

検定統計量の確率分布を明らかにする

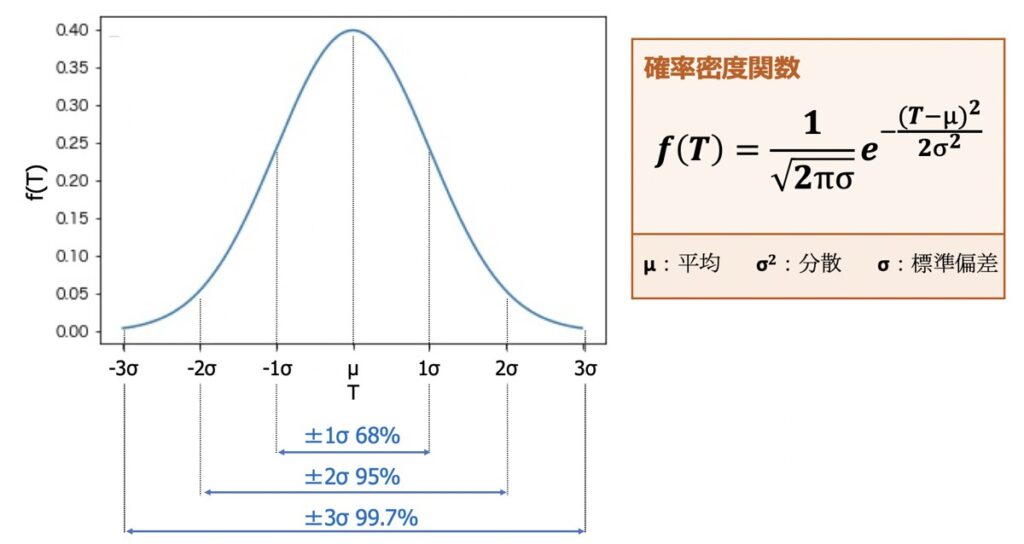
前述でも言及した通り、検定するために作成した検定統計量をT（X₁, X₂,・・・X_n）とおきます。確率変数Tが平均(μ)、分散(σ²)の正規分布に従うとき、上図のような確率分布が描画できます。

この分布をもとに帰無仮説の事象が起こる確率を計算します。

※確率分布の見方や正規分布の概要についてはこちらの記事で解説しています。

検定統計量が有意水準p以内であるか確認し、帰無仮説を棄却または採択する

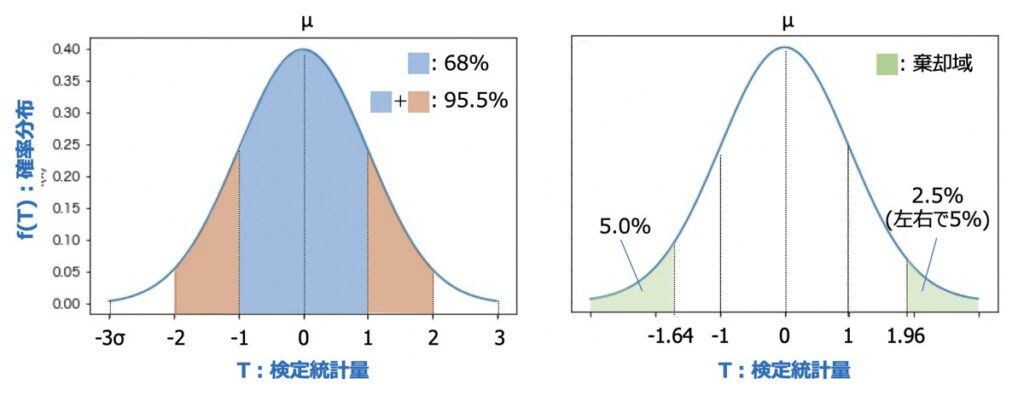
ソフトボール投げの問題において、帰無仮説の事象（小学2年生の男子生徒が遠投24mを記録）が起こる確率は、小学2年生の生徒全体の3%であることが分かったとします。

この問題の場合、検定統計量（T=3%）は有意水準（p=5%）より小さいため、帰無仮説H₀は間違ったものとし、対立仮説H₁を正しいものとして扱います。

これを「帰無仮説を棄却する」「対立仮説を採択する」と呼びます。

なお、検定統計量が有意水準p%以内となる範囲を棄却域と呼びます。加えて、優位水準p%より大きいとなる範囲は受容域と言います。

確率（検定統計量）がp以下の場合、帰無仮説を棄却し対立仮説を採択する
確率（検定統計量）がpより大きい場合、帰無仮説を採択する

【参考】両側検定と片側検定

棄却域を両側にとる検定を両側検定、棄却域を片側に取る検定を片側検定と言います。片側検定は棄却域の違いにより、上側検定と下側検定に分けられます。

母数ηの検定で、帰無仮説がη=aのとき対立仮説の取り方と棄却域の取り方は上図のようになります。

【事例】仮説検定

仮説検定の方法を詳しく理解するために、事例をいくつかご紹介します。

事例(1)｜仮説検定の概念理解

例題例題

ある箱の中に赤いボールと青いボールが入っています。無作為にボールを1つ取り出した時、そのボールが赤色である確率は3分の2であるという。

Aさんが3回ボールを取り出したところ、３回とも青色のボールであった。赤色のボールを取り出す確率が3分の2より小さいかどうか優位水準5%で検定せよ。

赤色のボールが取り出せる本当の確率をθと置きます。また、帰無仮説、対立仮説をそれぞれ次のように設定します。

帰無仮説	赤色のボールを引き当てる確率は2/3である	H₀ = 2/3
対立仮説	赤色のボールを引き当てる確率は2/3より小さい	H₁ < 2/3

帰無仮説のもとで1回のボール抽出で青色を引き当てる確率は次のように表されます。

青色を引き当てる確率：1 – 2/3 = 1/3

よって、3回とも青色を引き当てる確率は次のように表されます。

1/3 × 1/3 × 1/3 = 1/27 = 3.7 [%]

帰無仮説H₀が正しいという仮定のもとで、現実に起こった出来事が、どれくらいの確率で起こるのかを計算したのが上記の確率です。これが3.7%と非常に小さい確率であるため、帰無仮説H₀を疑うわけです。

小さい確率かどうかの判断の境目となるのが優意水準p値で、この問題の場合、5%と設定されています。3.7%は5%より小さいため、帰無仮説H₀を棄却し、対立仮説H₁はを採択します。

今回の例では帰無仮説が棄却されましたが、帰無仮説のもとで求められた確率の値が有意水準よりも大きい場合、帰無仮説を棄却することはできません。その場合、帰無仮説を採択します。

事例(2)｜母平均を検定

例題

Aさんは、全国の小学6年生男子のソフトボール投げの平均値は24.0m、標準偏差は6.0mであるとネットで調べた。ところが、Aさんの小学6年生の男子100人のソフトボール投げの平均値は25.5mであった。ネットで調べた標準偏差は正しい前提のもと、全国平均値24mは正しいかどうかを優位水準5%で検定せよ。なお、標本サイズは十分に大きいものとする。

例題の前提を整理すると、母集団と標本は次のように定義できます。

母集団	全国の小学校6年生男子全員のソフトボール投げの記録
標本	Aさんの小学校の男子生徒100人のソフトボール投げの記録

今回の例題は「母平均を検定する」ことが目的であるため、帰無仮説、対立仮説を次のように立てます。

帰無仮説H₀：θ = 24.0
対立仮説H1：θ ≠ 24.0

そして、標本平均が25.5m以上になる確率が5%以下であるか検証していきます。

母集団から100個抽出した時の値を独立な確率変数X₁, X₂, X₃・・・X₁₀₀と置くと、標本平均x̄は以下のように表せます。

x̄ = (X₁ + X₂ + ・・・ + X₁₀₀)/100

今回の例ではx̄が検定統計量になります。

続いて、x̄の確率分布を明らかにする上で、今回検定する母集団の真の平均値（母平均）をθと置きます。例題より、母集団の標準偏差は正しい前提であるため、母分散σ²はσ² = 6.0²と表せます。

母集団から抽出した確率変数X_iに対して、標本平均の期待値E[X_i]、分散V[X_i]は次のように表せます。

E[X_i]=θ
V[X_i]=6.0²

例題の前提により標本サイズ100は十分大きいと捉えるため、中心極限定理によりx̄の分布は正規分布N(μ, 6.0²/100)に従うとみなして良いことになります。

帰無仮説のもとでx̄の分布はN(24.0, 6.0²/100)となります。

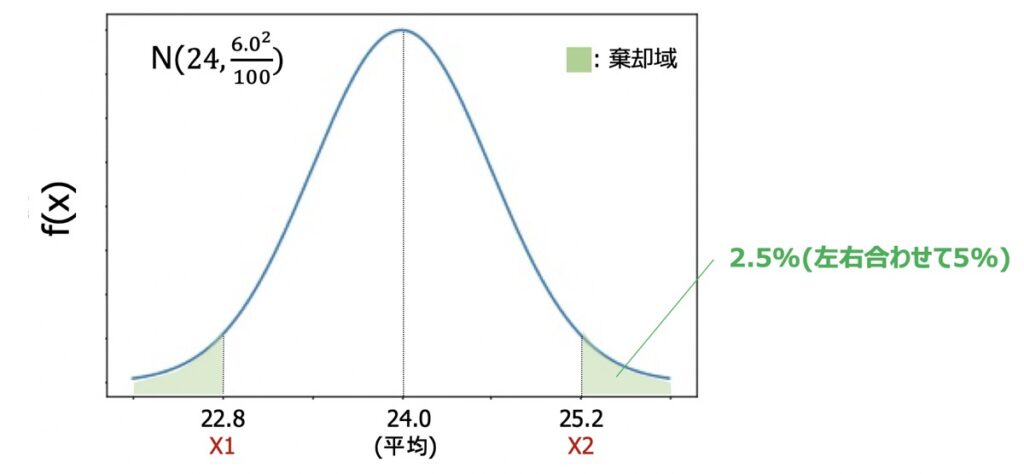
図のように検定方法は両側検定とした場合、棄却域を両側合わせて5%の面積とするために、境界線となるX₁、X₂を求めます。

正規分布の表を参照いただくと、両側それぞれで2.5%に対応する値は1.96であるため、X₁およびX₂は次のように表されます。

X₁： 24.0 – 1.96 × (6²/100) = 22.8
X₂： 24.0 + 1.96× (6²/100) = 25.2

上記の結果、帰無仮説を棄却または採択する基準は、次のように表せます。

帰無仮説H₀を棄却する	x̄<=22.8 または x̄ >= 25.2
帰無仮説H₀を受容する	22.8 < x̄ < 25.2

Aさんの小学校の6年生男子100人の平均値25.5は25.2よりも大きいため、有意水準5%以内の範囲に入っていることが分かります。

つまり、x̄が25.5以上になる確率は5%よりも小さいため、帰無仮説H₀を棄却します。結果、優位水準5%で全国の小学校6年生男子のソフトボール投げの平均値が24.0mでないことが分かりました。

【参考】仮説検定を学習する上でおすすめの教材

仮説検定を学習する上でのおすすめ教材をご紹介します。是非参考にしてみてください。

【参考】検定統計量および仮説検定の種類

実際の仮説検定の場面では、次のような検定統計量が代表的に用いられます。

代表的な検定統計量

z値
t値
F値
カイ二乗値

代表的な検定統計量の算出および確率分布を求める方法は以下の記事で詳しく解説しています。

さらに、前述の検定統計量を用いて以下のような検定を実施します。

t検定	・２グループ間での平均値の差を検定
カイ二乗検定	・関係性（影響）の有無を検定・母分散の検定、分布の適合度検定など
分散分析	・２つ以上のグループ間の差の検定