こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- 機械学習モデルにおける説明変数選択法について理解したい
- ステップワイズ法と強制投入法について詳しく理解したい
ステップワイズ法とは

ステップワイズ法とは、機械学習モデルのインプットとして投入した説明変数の中から、目的変数と関連度の高い(=スコアの高い)説明変数のみを自動で取捨選択してくれる方法を指します。
ステップワイズ法の種類
ステップワイズ法は、説明変数の選択プロセスの違いから以下の種類に細分化されます。
| 変数選択法 | 意味 |
|---|---|
| 変数増加法 (Forward Selection Method) | 説明変数を持たない空のモデルに対して、スコアの高い順に1つずつ説明変数を追加していく方法。 |
| 変数減少法 (Backword Selection Method | 説明変数を全て投入したモデルから、スコアの低い順に1つずつ説明変数を除外していく方法。 |
| 変数増減法 (Stepwise Forward Selection Method) | 変数増加法と変数減少法を組み合わせた方法。 変数増加法を基準としながら説明変数を増やしつつ、変数減少法を併せて適用。 |
| 変数減増法 (Stepwise Backward Selection Method) | 変数増加法と変数減少法を組み合わせた方法。 変数減少法を基準としながら説明変数を減らしつつ、変数増加法も併せて適用。 |
ステップワイズ法というと、論文等では主に「変数増減法」を指して言及されることが多いです。
ステップワイズ法|変数選択スコアの算出方法
ステップワイズ法では、説明変数と目的変数の関連度をスコアとして算出し、高いスコアを示した説明変数を優先的に選択する仕組みとなっています。
この時の評価指標として用いることができるスコアには次のようなものがあります。
| スコア | 概要 | 対象モデル |
|---|---|---|
| F検定有意確率 | 有意確率が低いほどスコアが高いと判断 | 線形回帰 |
| 偏相関 | 第三の交絡因子による影響を取り除いた2つの変数間の相関 | 線形回帰 |
| Wald統計量 | (回帰係数÷標準誤差)の2乗として算出した検定統計量 | ロジスティック回帰 |
| 尤度比 | 感度と特異度の比として表した統計量 | ロジスティック回帰 |
変数増減法(Stepwise Forward Selection Method)
変数増減法とは、変数増加法と変数減少法を組み合わせた方法を指します。変数増加法をもとに説明変数を増やしつつ、変数減少法を併せて適用します。
変数増減法では、まず、説明変数を用いない空のモデルを作成します。続いて、変数増加法をもとに説明変数と目的変数の関係を明らかにするために1つずつ回帰分析を行い、併せて前述のスコアを算出します。スコアが最も高い説明変数から逐次的にAI・機械学習モデルへと追加していく流れとなります。
ここで、スコアが高い説明変数追加の流れは変数増加法と同じですが、変数増減法の場合、事前に説明変数を取捨選択するためのスコアの基準(閾値)を定義するという違いがあります。このスコアの閾値を用いて、閾値以下となった説明変数は併せてモデル投入変数候補から除外していくという処理を実施しています。
このように、変数増加法をもとにスコアが高い説明変数を追加していきつつ、スコアが閾値以下を示した説明変数も併せて除外し、最終的に説明変数が追加・除外できなくなったタイミングで説明変数選択プロセスを終了する変数選択法を変数増減法といいます。
変数減増法(Stepwise Backward Selection Method)
変数減増法とは、変数増加法と変数減少法を組み合わせた方法を指します。変数減少法を基準としながら説明変数を除外しつつ、変数増加法を併せて適用します。
変数減増法では、まず、説明変数を全て投入したモデルを作成します。続いて、変数減少法をもとに説明変数と目的変数の関係を明らかにするために1つずつ回帰分析を行い、前述したスコアを算出します。スコアが最も低い説明変数から逐次的に除外していく流れとなります。
ここで、スコアが低い説明変数除外の流れは変数減少法と同じですが、変数減増法の場合、除外した説明変数を復活させるためのスコアの基準(閾値)を定義するという違いがあります。このスコアの閾値を用いて、閾値以上となった説明変数は併せてモデルに再追加していくという処理を実施しています。
このように、変数減少法をもとにスコアが低い説明変数を除外していきつつ、除外された説明変数の中からスコアが閾値以上を示した説明変数は併せて再追加していき、最終的に説明変数が追加・除外できなくなったタイミングで説明変数選択プロセスを終了する変数選択法を変数減増法といいます。
ステップワイズ法のメリット・デメリット
ステップワイズ法のメリットとデメリットについて以下解説します。
【メリット】モデル性能向上に有効な説明変数を自動で選択できる
AI・機械学習モデル作成における重要なプロセスの1つに「説明変数選択」があります。
候補となる説明変数が多い場合、1つずつ手動で説明変数vs目的変数の寄与度を検証していては非常に手間がかかりますね。このような時に役立つのがステップワイズ法です。
ステップワイズ法は検定統計量に基づき定量的に有効な説明変数を評価・選択してくれます。加えて、多重共線性などモデル性能に悪影響を及ぼす要因も検出し、対象となる説明変数は除外してくれます。
【デメリット】モデル作成に至るまでの処理が遅くなる
ステップワイズ法は、モデル投入に際して説明変数の有効性を1つずつ検証していくプロセスがあります。そのため、説明変数の候補が多くなるほど計算量が増加するため、モデル作成に至るまでの処理が遅くなる傾向にあるのです。
スコアの算出方法によってこの処理速度はある程度対策できますが、基本的にステップワイズ法で処理速度が速いスコア算出方法を採用するということは、有効な説明変数を選択するための「正確さ」が犠牲になっていると言えます。説明変数選択に際する「正確さ」と「処理速度」はトレードオフの関係にある点も考慮しましょう。
強制投入法(総当たり法)
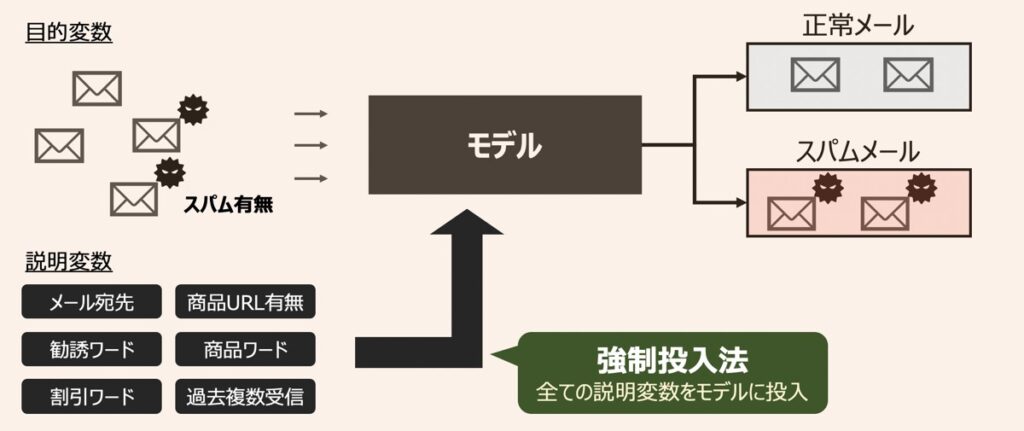
ステップワイズ法としばし比較される方法として強制投入法があります。強制投入法とは、全ての説明変数をAI・機械学習モデルに投入する手法を指します。
強制投入法のメリット・デメリット
【メリット】ステップワイズ法と比較して処理速度が速い
強制投入法の場合、説明変数を「選択する」というプロセスがなく、全ての説明変数を投入することになるため、後続のモデル作成における処理速度はステップワイズ法を採用した場合と比較して圧倒的に速くなる傾向があります。
【デメリット】AI・機械学習モデルのノイズとなる説明変数を除外できない
ステップワイズ法の場合、目的変数との相関性や多重共線性等を考慮した有効な説明変数が選択されます。一方で、強制投入法の場合はこれらが考慮されていないため、別途回帰分析というタスクを設けて対応する必要があります。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




