こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
正則化とは|過学習への対策
過学習とは
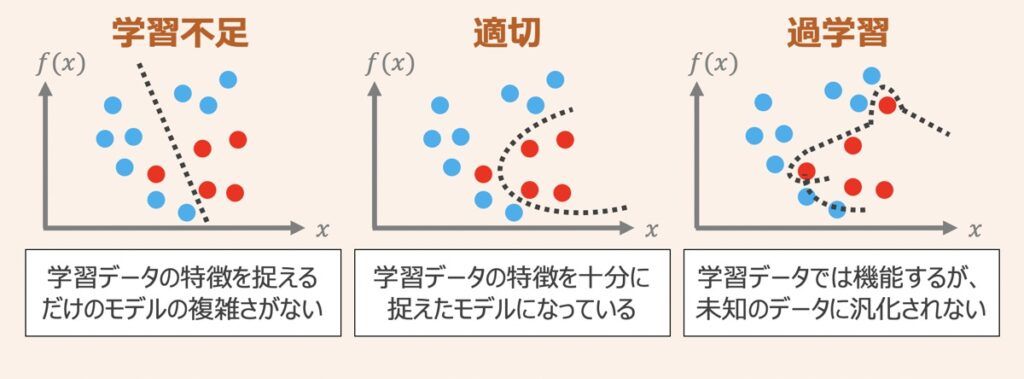
機械学習モデルを開発する上で、過学習対策はモデル性能改善に欠かせない重要課題です。
上図のように機械学習モデルを作成し、学習データに対してモデルパラメータがうまくフィッティングするよう学習したとします。この時、学習データに対するモデルの表現力が高ければ高いほど,学習データに対してのみ過剰に当てはまりが良くなる状態になってしまい、テストデータへの当てはまりが悪くなる「過学習」の状態に陥ってしまいます。
正則化による過学習の対策
正則化とは、過学習対策の手法であり、学習データへの過剰フィッティングに伴うモデル複雑化を抑制しながら、より単純な(低い次元の)モデルとして学習データを表現できることを目指したものです。
高次元データをモデルに適用した場合に発現する高次元学習問題では、説明変数が多い分モデルの複雑さが増す傾向にあるため、特に正則化が有効であると言えます。
正則化の概念的な理解
正則化の具体的な仕組みは、パラメータ(重み)にペナルティを科すための追加情報(バイアス)を導入することで、モデルの複雑性と学習データへの当てはまりの良さをバランスさせ、過学習対策を行います。
上記理解のために、まず学習データを用いた一般的なモデル学習ケースを考え、モデル性能を改善するために予測性能誤差Eを最小化することを検討しましょう。
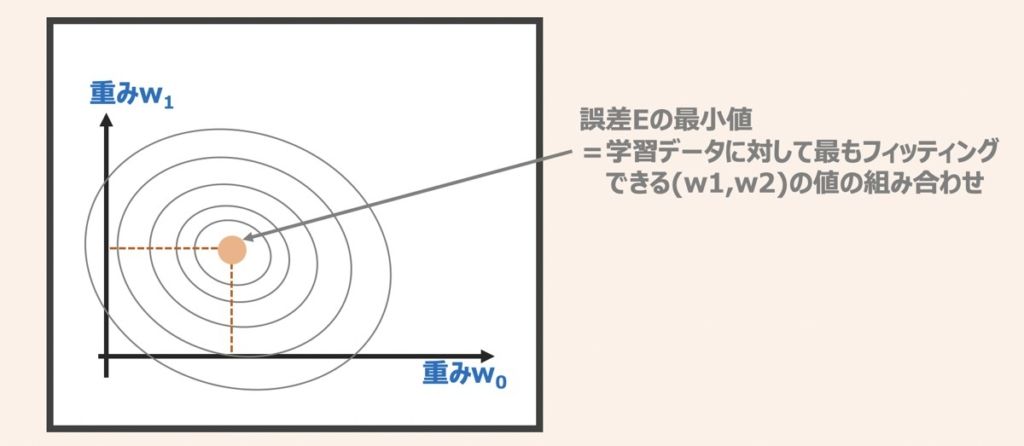

上図より、モデルの予測性能誤差Eが最小(学習データに対して最も当てはまりが良い)となる重み係数(w0,w1)の組み合わせを見つけ出すイメージを解説します。
この時、上図中心の座標(オレンジプロット)がモデルの誤差Eが最小となる(w0,w1)の座標位置だとします。
モデルの精度の追求するならば、オレンジプロット(w0,w1)を重み係数を値として採用し、モデルに用いるのが良いと言えます。一方でこの場合、過剰フィッティングした過学習の状態に陥る懸念があります。
そこで上図に対して「ペナルティを科すことでモデルの過学習を抑制する」という正則化について考えます。
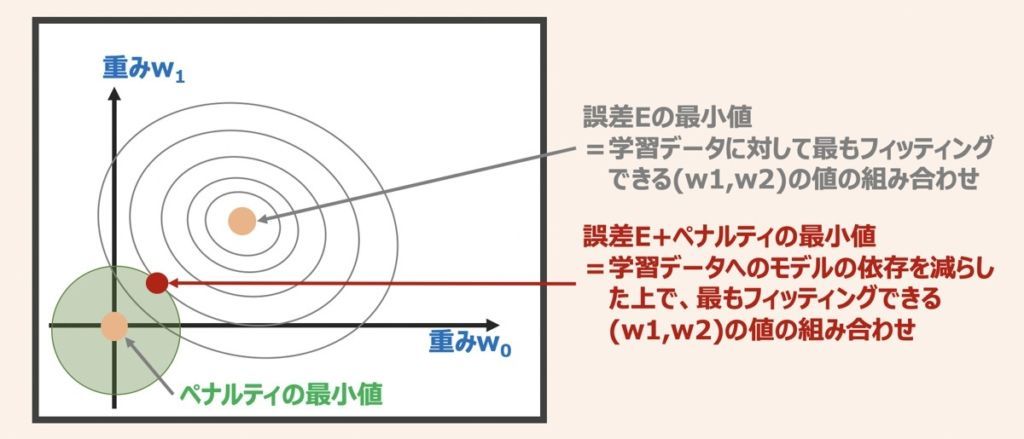

正則化を適用すると、上図のように小さい重みを促すペナルティ項(緑円)を追加したイメージになります。これは、重み係数(w0,w1)が取りうる範囲を緑円内に制限することを意味します。結果、大きな重みがあるとその分ペナルティを科されることになります。
以上より学習データセットへのモデルの依存を減らすことができるようになるわけです。
L2正則化とL1正則化

機械学習では、L1正則化とL2正則化という手法が一般的に用いられます。これら概要について後述します。
L2正則化(L2 regularization)
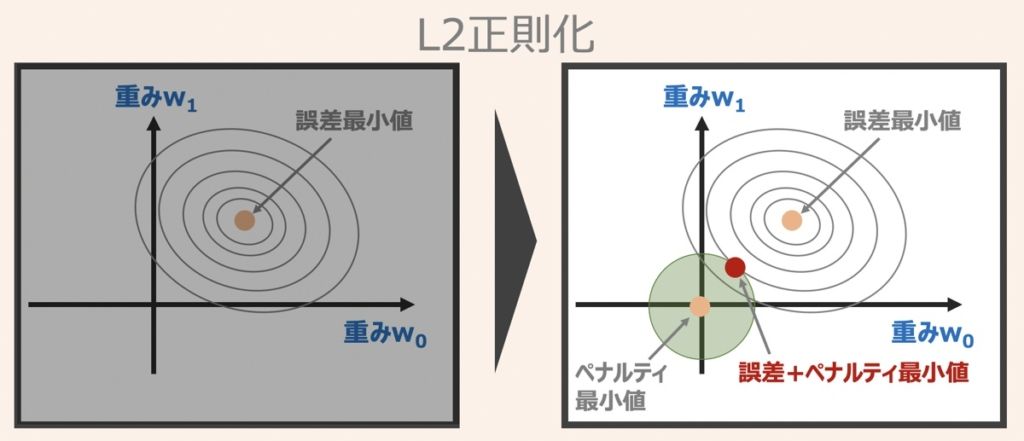

L2正則化の概念図およびペナルティ項の式は上図のように示されます。
L2正則化の場合、重み係数(w0,w1)が取りうる範囲は緑の円内に限られます。正則化パラメータλは任意に設定することができ、λの値を大きく設定するほど、ペナルティ項(緑の円)は小さく縮小し、λ=∞の場合は重み係数(w0,w1)=(0,0)となります。
機械学習の世界では、後述するL1正則化に比べ、L2正則化の用いられる頻度が多いように見受けられます。
L1正則化(L1 regularization)
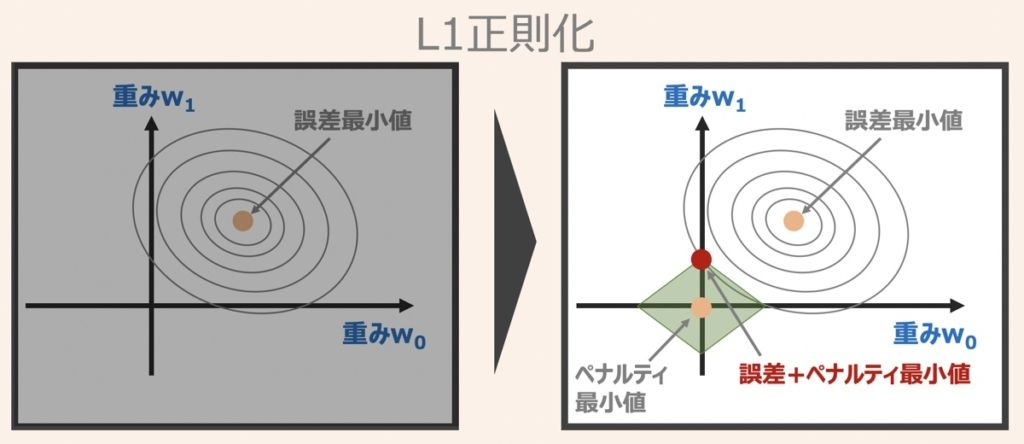

L1正則化の概念図およびペナルティ項の式は上図のように示されます。
L1正則化の場合、重み係数(w0,w1)の取りうる範囲はひし形として表されるイメージです。またL1正則化のペナルティは重み係数の絶対値の和として表されます。
さらにL1正則化の特徴として、重み係数(w0,w1)が最適となる組み合わせは、ひし形で示す角部分となることが多いです。これは、あまり重要でない説明変数の係数(重み)をゼロにすることを意味します。つまり、L1正則化による重みの最適化条件は疎性を促すと言えます。
L1正則化を適用すると、本当に必要な変数だけモデルに利用されるため、モデル開発者がどの変数が重要か認識しやすくなります。
ただし、一般的にはL2正則化の方が予測の性能は高いと言われており、この点考慮が必要です。
【参考】AI・機械学習における配信情報まとめ
当サイトではAI・機械学習における「基礎」から「最新のプログラミング手法」に至るまで幅広く解説しております。また「おすすめの勉強方法」をはじめ、副業・転職・フリーランスとして始める「AI・機械学習案件の探し方」についても詳しく言及しています。
【仕事探し】副業・転職・フリーランス
【教育】おすすめ勉強法
【参考】記事一覧
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら




