【統計学基礎】正規分布とは｜Pythonでの描画方法も徹底解説

2022年5月26日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

こんな方におすすめ

正規分布の概要を詳しく理解したい
Pythonを用いて正規分布を描画する方法が知りたい

正規分布とは｜Normal Distribution

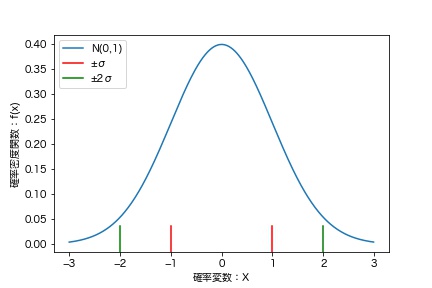
正規分布（ガウス分布）は最も汎用的に利用される重要な分布の1つであり、社会科学、自然科学など世の中の事象を簡単に表現するためのモデルとして利用されています。

正規分布は平均を中心に左右対称のつりがね型の分布を取るのが特徴であり、その他にも次のような特徴があります。

平均値を中心に曲線は左右対称となる
ピークは平均の値となる
平均値、中央値、最頻値が一致する
標準偏差が曲線の形状を決める
標準偏差が小さいほど曲線のピークは鋭くなり、分布の幅は狭くなる
標準偏差が大きいほど曲線のピークは平らになり、分布の幅は左右広がった形状となる
X軸が漸化式を示す
曲線のしたの面積（AUC）は1を示す

正規分布の確率密度関数

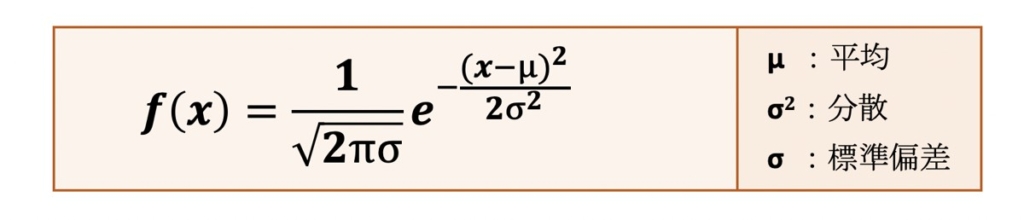
1変量確率変数xが平均(μ)、分散(σ²)の正規分布に従うとき、その確率密度関数は上記のように表せされます。

正規分布は、平均μ、分散σ²に従うこととき、N(μ,σ²)に従うとしばし表記されます。このNは正規分布（Normal Distribution）のアルファベット表記から来たものです。

正規分布の確率密度関数の総和は1であり、全区間で積分すると1になる特徴があります。

正規分布の特徴

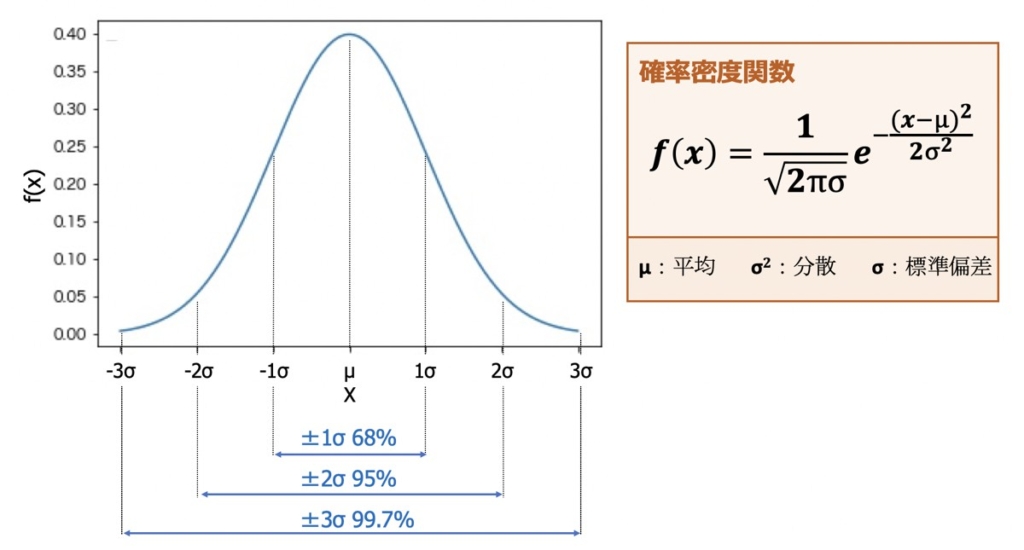
正規分布は「正規分布は、平均(μ)と標準偏差(σ)が分かると、確率変数Xの発生確率が分かる」という重要な特性を有しています。

上図に示す正規分布のグラフは、標準偏差（±1σ、±2σ、±3σ）の範囲を示して描いたものです。

全ての正規分布は、平均、分散、標準偏差の値に依存せず、次のような特性を示します。このような特徴は、検定に応用する際に非常に有効です。

確率変数Xの範囲	変数Xの発生確率
– 1σ <= X <= 1σ	全体の68%
– 2σ <= X <= 2σ	全体の95%
– 3σ <= X <= 3σ	全体の99.7%

【参考】Python×統計学の学習におすすめな教材

「データ分析する上で統計学の基礎を学びたい」「Pythonで動かしながら統計解析を学びたい」方向けに以下の教材をおすすめします。

データ分析で必須の統計学基礎を学びたい方向け

Pythonと併用して統計解析を学びたい方向け

Pythonで実際に動かしながら学習することで、プログラミングに加え、統計学の応用も合わせた深い知識習得が期待できます。

標準正規分布

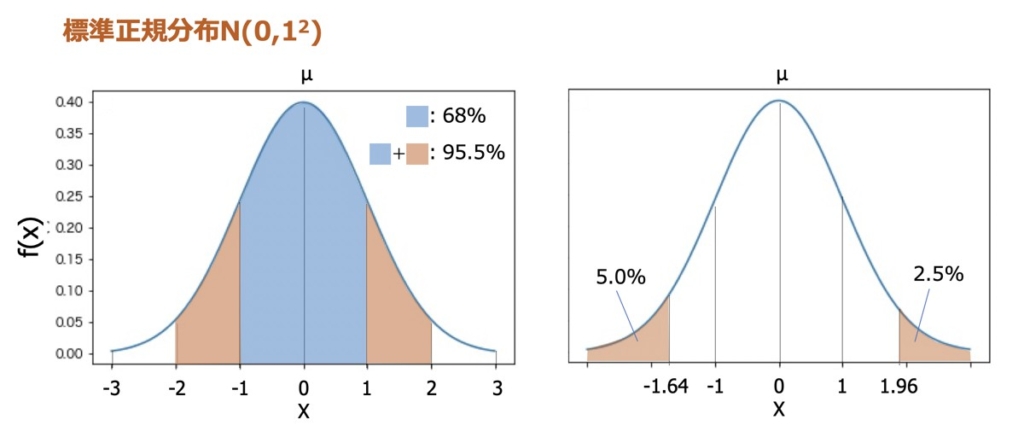
確率変数Xの平均μ = 0分散 σ²=１の場合の正規分布を標準正規分布といい、異なる尺度の分布を比較する際によく利用されます。

標準正規分布の確率密度関数のグラフは上記のようになります。曲線とX軸で挟まれた面積を100%とした時、左図の-1〜1間の面積は全体の68%になることを示しており、-2〜2間になると全体の95.5%になることを示しています。

また、右図の-1.64以下の面積は全体の5%になることを示し、1.96以上の部分は全体の2.5%になることを示しています。これら代表値は仮説検定の際しばし利用するものであるため、覚えておくと便利です。

標準正規分布の確率密度関数

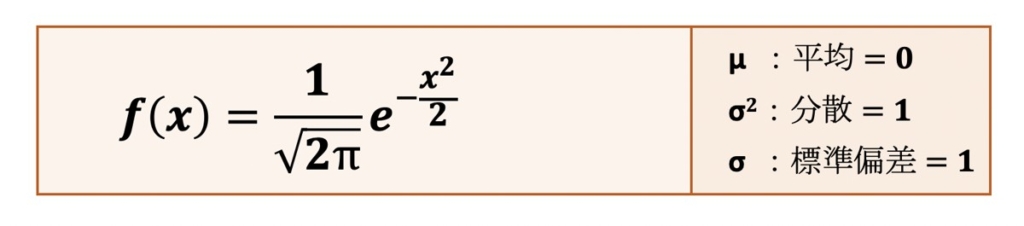
Z値｜標準正規分布への変換方法

全ての正規分布は標準正規分布への変換が可能です。この変換は正規分布の標準化と呼び、上記の式を用いて実行されます。

手順で記述すると以下のようになり、標準化したデータはzスコア（z値）と呼ばれます。

Xと平均の差を計算する
Xと平均の差を標準偏差で割る

中心極限定理

平均(μ)、分散(σ²)である母集団から無作為に抽出する標本Xの分布は、サンプルサイズnが大きくなるにつれて、平均(μ)、分散(σ²/n)の正規分布N(μ, σ²/n)に近づきます。これを中心極限定理と言います。

この定理の存在よって、正規分布があらゆる場面で使える分布となっています。一方で、標本の分布に分散が存在しない場合、必ずしも正規分布に従わない場合もあります。

正規分布の例

全国の小学生の身長
全国模試の成績（点数）
全国の小学6年性の50m走のタイム

正規分布と推定統計

推測統計では、正規分布に従う母集団の平均や分散を標本の平均や分散をもとに推測します。ここで、標本平均や分散をそのまま母集団の平均や分散の予測値として使うことも可能ですが、標本の平均や分散を確率分布として捉えることで、より精細に母集団の平均や分散の確らしさを検証できるようになります。ここで用いる代表的な分布としてカイ二乗分布、t分布、F分布があります。

【参考】推測統計で用いる代表的な分布

母集団が正規分布に従うものとした場合、次のような標本の確率分布が得られます。

カイ二乗分布	標本の偏差平方和が従う確率分布
t分布	標本平均を標本の分散で標準化した値が従う確率分布
F分布	母分散が等しい2つの標本の分散比が従う確率分布

【Python】正規分布を描く方法

Pythonを用いて正規分布を描画する方法について解説します。

scipy｜正規分布の可視化方法

正規分布はscipyを用いて描画できます。

以下は平均0、標準偏差1の標準正規分布を描くためのコードを示します。

# 正規分布
from scipy import stats
# 分布の可視化
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams
rcParams["font.family"]     = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"
# %matplotlib inline

"""
**************************************
データの準備
**************************************
"""
# 標準正規分布を描画
mean = 0   # 平均    = 0
std  = 1   # 標準偏差 = 1

# 変数Xの領域を任意に決定
X = np.arange(-3,3,0.01)

# 確率密度関数Yを計算
Y = stats.norm.pdf(X,mean,std)


"""
**************************************
正規分布を描画
**************************************
"""
# 正規分布を描画
plt.plot(X,Y,label="N(0,1)")

# 標準偏差
plt.axvline(x=std   ,color="red",   ymax=0.3*Y.max(), label="±σ")
plt.axvline(x=-std  ,color="red",   ymax=0.3*Y.max())
plt.axvline(x=2*std ,color="green", ymax=0.3*Y.max(), label="±2σ")
plt.axvline(x=-2*std,color="green", ymax=0.3*Y.max())

# グラフ書式設定
plt.xlabel("確率変数：X")
plt.ylabel("確率密度関数：f(x)")
plt.legend(loc="upper left")
plt.show()

平均meanと標準偏差std部分を修正することで、目的の正規分布が描画できます。ぜひ色々と試してみてください。