【統計学×Python】相関分析とは｜相関係数算出と分布可視化方法も徹底解説

2022年5月24日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

こんな方におすすめ

相関・相関分析とは何か詳しく知りたい
相関分析に用いる統計量の数学的背景が知りたい
Pythonを用いて相関係数を算出し、相関分布を描画する方法が知りたい

相関とは

２変量のデータ（X, Y）について、Xの増減とYの増減に関係性が認められる場合、この関係性を相関といいます。

例えば、スマホを見る時間（X時間）と学校のテストの成績（Y点）を調べたデータがあるとします。スマホを見る時間（X）が長ければ長いほど、テストの成績（Y）は下がるという相関関係が認められるでしょう。

また、気温（X度）とアイスクリームの購入者数（Y人）であれば、気温(X)が高くなればアイスクリーム購入者数（Y）も増加するという相関関係が認められます。

相関分布の種類

正の相関	ある値が増加すると、もう一方の値も増加
負の相関	ある値が減少すると、もう一方の値は減少
無相関	ある値の増減がもう一方の値に影響しない

上図のように、XとYの関係を散布図で表すと、2変数間の相関性を視覚的に確認できるようになります。

この分布から、Xの増減に伴いYも増減することが分かる場合、XとYには相関があると推察できます。

反対に、Xの増減がYの値に影響しない場合は、XとYは相関がない（無相関）と判断できます。

相関係数

相関係数とは、２変数間の相関の強さを示した統計学的指標です。

前述の相関分布を見ると、視覚的に相関があることが確認できました。一方で、目視確認だと相関の判断が主観的になってしまいます。そこで、相関の度合いを数値で表し、客観的評価を可能にしたのが相関係数になります。

相関係数は単位ではなく、-1～1の範囲の値として示されます。１に近づくほど正の相関が強く、-1に近づくほど負の相関が強いと判断します。また、相関係数が0に近い値をとる場合、相関がないと判断します。

相関係数	解釈目安
±0.7～±1.0	強い相関
±0.5～±0.7	中程度の相関
±0.3～±0.5	弱い相関
0～±0.3	ほとんど相関無し

疑似相関

相関係数を調べて結果を考察する場合、注意すべき観点として「疑似相関」があります。

相関関係が強い2変数同士であっても、その2つの変数間に因果関係があるとは限りません。

因果関係とは

2つの変数において、一方の変数が原因を指し、他の一方の変数はその結果という繋がりを有する関係

例えば、ある小学校1学年〜6学年の生徒に共通の英語テストを受けてもらったとします。その結果、小学生の身長をX、英語の成績をYとして統計を見ると、身長(X)が高いほど英語の成績(Y）が良いという相関が認められました。

これは、年齢（学年）が上がるにつれて身長(X)も伸び、年齢とともに英語の知識も深くなるため、英語の成績（Y）も良くなったという背景が隠れています。つまり、身長の伸びが原因で、英語の成績が良くなったわけではありません。

今回の例の場合、XとYの他に年齢（Z）という変数が隠れています。「年齢(Z)の増減が原因で、XとYという結果が表れる」という因果関係になっているわけです。XとYには相関関係があっても、直接の因果関係はありません。このような相関をみかけの相関または疑似相関といいます。

相関係数の種類・計算方法

相関係数には、数学的背景および計算方法の違いから次のような種類があります。

ピアソンの相関係数
ケシドールの順位相関係数
スピアマンの順位相関係数
自己相関係数
クラメールの連関係数

一般的な相関係数だとピアソンの相関係数を指すことが多いです。後述ではピアソンの相関係数について数学的背景を解説します。

ピアソンの相関係数(Correlation Coefficient)

ピアソンの相関係数r_xyは、共分散をそれぞれの変数の標準偏差で割ることで算出できます。

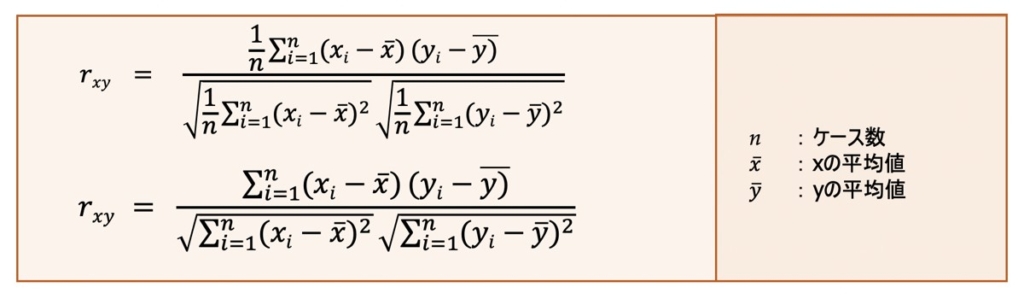
【実践】Pythonで相関分析｜相関係数の算出および相関分布の可視化

Python環境で「相関係数の算出」および「相関分布を可視化」する方法について以下解説します。

データの準備

相関分析に際して、以下のデータを活用します。

とあるコンビニでの「気温」に伴う「アイスクリーム」「おでん」「ビール」の売上実績を示したデータです。

import pandas as pd

# とあるコンビニのデータ
temperature = [ 5, 12, 16, 20, 24, 27, 29, 31, 33]  # 月平均気温
ice_cream   = [ 8,  8,  9, 13, 15, 19, 25, 29, 36]  # アイスクリームの月間売上
oden        = [19, 17, 12,  9,  5,  6,  4,  5,  3]  # おでんの月間売上
beer        = [10, 10,  9, 10,  8,  9, 10,  9, 11]  # ビールうの月間売上

# データフレーム
df = pd.DataFrame({"気温[度]":temperature,
                   "アイス売上[万円]":ice_cream,
                   "おでん売上[万円]":oden,
                   "ビール売上[万円]":beer,
                  })

# 出力
print(df)

# 出力イメージ
#    気温[度]  アイス売上[万円]  おでん売上[万円]  ビール売上[万円]
# 0      5              8             19             10
# 1     12              8             17             10
# 2     16              9             12              9
# 3     20             13              9             10
# 4     24             15              5              8
# 5     27             19              6              9
# 6     29             25              4             10
# 7     31             29              5              9
# 8     33             36              3             11

相関係数を算出

変数間の相関係数を算出する場合、データフレーム(df)に対してcorr()メソッドを適用します。

# 相関係数算出
print(df.corr())

# 出力イメージ
#                   気温[度]  アイス売上[万円]  おでん売上[万円]  ビール売上[万円]
# 気温[度]          1.000000      0.896062     -0.969815       -0.021749        ★着目
# アイス売上[万円]   0.896062      1.000000     -0.815905        0.295804
# おでん売上[万円]  -0.969815     -0.815905      1.000000        0.134331
# ビール売上[万円]  -0.021749      0.295804      0.134331        1.000000

★の行に着目すると、「気温vsアイス」および「気温vsおでん」では強い相関性が示唆されます。一方で、「気温vsビール」ではほとんど相関性が無いと言えます。

ヒートマップで相関係数を可視化

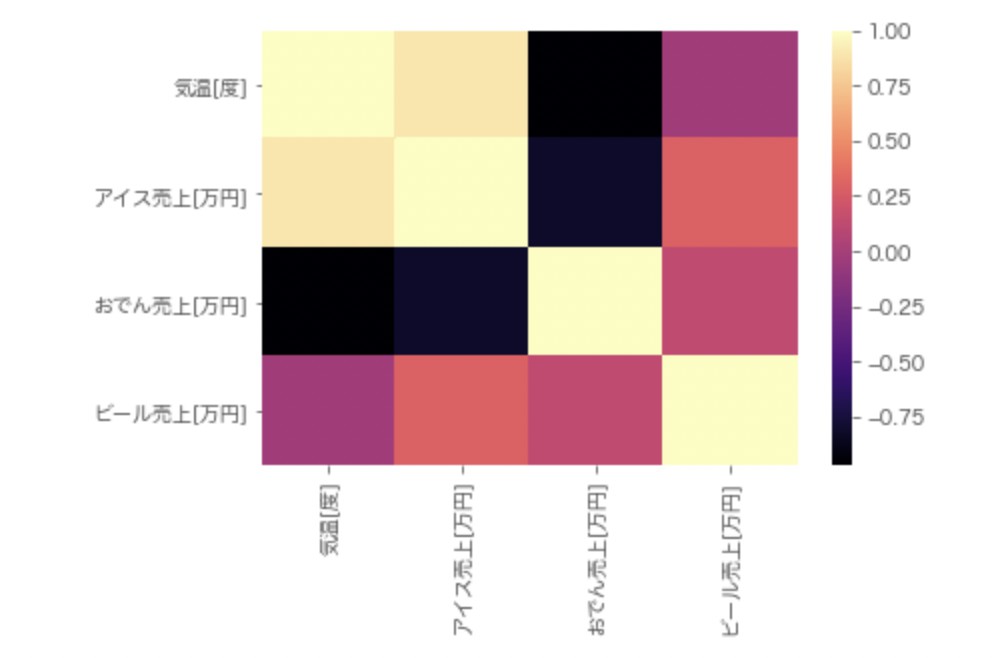
上図のようなヒートマップを用いて相関係数を可視化したい場合、以下のように記述します。

# グラフ可視化ライブラリ
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import rcParams

# 日本語対応
rcParams["font.family"]     = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"

# ヒートマップ
sns.heatmap(df.corr(),     # 各種変数間の相関係数
            cmap="magma"   # カラーマップ
           )

散布図で相関分布を描画

2変数間の相関分布を描画したい場合、散布図が有用です。以下のコードを実行してみましょう。

# グラフ可視化ライブラリ
import matplotlib.pyplot as plt
from matplotlib import rcParams

# 日本語設定
rcParams["font.family"]     = "sans-serif"
rcParams["font.sans-serif"] = "Hiragino Maru Gothic Pro"


# グラフ可視化
plt.scatter(
            df["気温[度]"],          # X軸値
            df["アイス売上[万円]"],    # Y軸値
            marker = "o",           # マーカー形状
            s = 100,                # プロットサイズ
            c = "blue",             # カラー
            edgecolor = "black",    # 枠線カラー
            linewidth = 1,          # 線の太さ
            alpha = 0.4,            # 透明度
            )

# 書式設定
plt.xlabel("気温[度]")               # X軸ラベル
plt.ylabel("アイス売上[万円]")        # Y軸ラベル
plt.show()

Pythonで散布図を描く具体的な方法についてはこちらの記事で解説しています。