こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
- t検定の基本的な考え方から、使い方、種類、具体的な事例を詳しく学びたい
t検定
t検定とは、2つの平均値の差が偶然によるものか、統計的に有意な差があるのかを判断する手法です。
たとえば「新しい薬を使ったグループ」と「使っていないグループ」の効果を比べたいときなどに使われます。
平均の差を見るといっても、サンプルにはバラつき(分散)があるため、単純な差だけで判断するのはNG。そこで、サンプル数やばらつきを加味したt値という指標を計算し、それが偶然に起こりうる範囲なのかを判断します。
このとき「偶然の範囲ではなさそうだ」と判断できれば、「2つの平均に有意な差がある」と言えるわけです。
t検定のパターン
t検定には、主に以下の3つのパターンがあります。
対応のない2群のt検定(独立2群のt検定)
別々の2つのグループの平均値を比べるときに使います。たとえば「男性と女性でテストの平均点が違うか」を知りたいときなど。
対応のあるt検定(対応のある2群のt検定)
同じ対象に対して、前後比較をしたいときに使います。たとえば「ダイエット前後で体重が変化したか」など、同一人物を比較する場面に適しています。
一標本のt検定
1つのグループの平均値が、特定の基準値(母平均)と異なるかを検定します。たとえば「平均身長が日本の平均170cmと比べて違いがあるか?」など。
t検定の流れ
t検定を行う際の基本的な流れは、大きく5つのステップに分かれます。それぞれのステップが何を意味しているのかを、わかりやすく見ていきましょう。
1. 仮説を立てる(帰無仮説と対立仮説の設定)
最初に行うのは、「どんな差を検証したいのか?」という仮説の設定です。統計学では、必ず2つの仮説を立ててから検定を行います。
- 帰無仮説(H₀):「2つの平均に差はない」とする仮説。これが正しいとみなして検定を始めます。
- 対立仮説(H₁):「2つの平均に差がある」という仮説。帰無仮説が間違っているとしたときに成り立つ仮説です。
たとえば、新しい薬の効果を調べる場合は、
- H₀:「新薬と従来薬の効果に差はない」
- H₁:「新薬は従来薬よりも効果がある」
というように設定します。
2. 有意水準を決める(αの設定)
次に、「どのくらいの確率まで誤差を許すか?」という基準=有意水準を決めます。これは、**帰無仮説が正しいのにそれを間違って棄却してしまうリスク(第1種の過誤)**をどこまで許容するかを意味します。
一般的には、
有意水準 α = 0.05(=5%) がよく使われます。
これは「100回中5回は間違って差があると判断してしまうかもしれない」という意味です。より厳密に判定したい場合は、α = 0.01(=1%)など、低い水準を使うこともあります。
3. t値を計算する(統計量の算出)
次に行うのが、実際にデータからt値(検定統計量)を計算するステップです。これは、2つの平均の差が、標準誤差(ばらつきの大きさ)に対してどれくらい大きいかを測る指標です。

このt値が大きければ大きいほど、「平均に差があるかもしれない」という判断につながります。
4. p値を求める(確率で判断)
t値をもとに、p値と呼ばれる数値を求めます。p値とは、「帰無仮説が正しいとした場合に、今回のような結果が偶然に起こる確率」を意味します。
このp値と、先に決めた有意水準(α)を比較して判断します。
- p値 < 有意水準 → 有意差あり(帰無仮説を棄却)
- p値 ≥ 有意水準 → 有意差なし(帰無仮説を採択)
たとえば、p値が0.03で、有意水準を0.05に設定していた場合、「統計的に有意な差がある」と結論づけられます。
5. 結果を解釈する
最後に、検定結果をもとに結論を導きます。「差がある/差がない」だけではなく、その差がどの程度の大きさか(効果量)や、実際に意味のある差かどうか(実務的意義)も合わせて考えると、より説得力のある分析ができます。
t分布
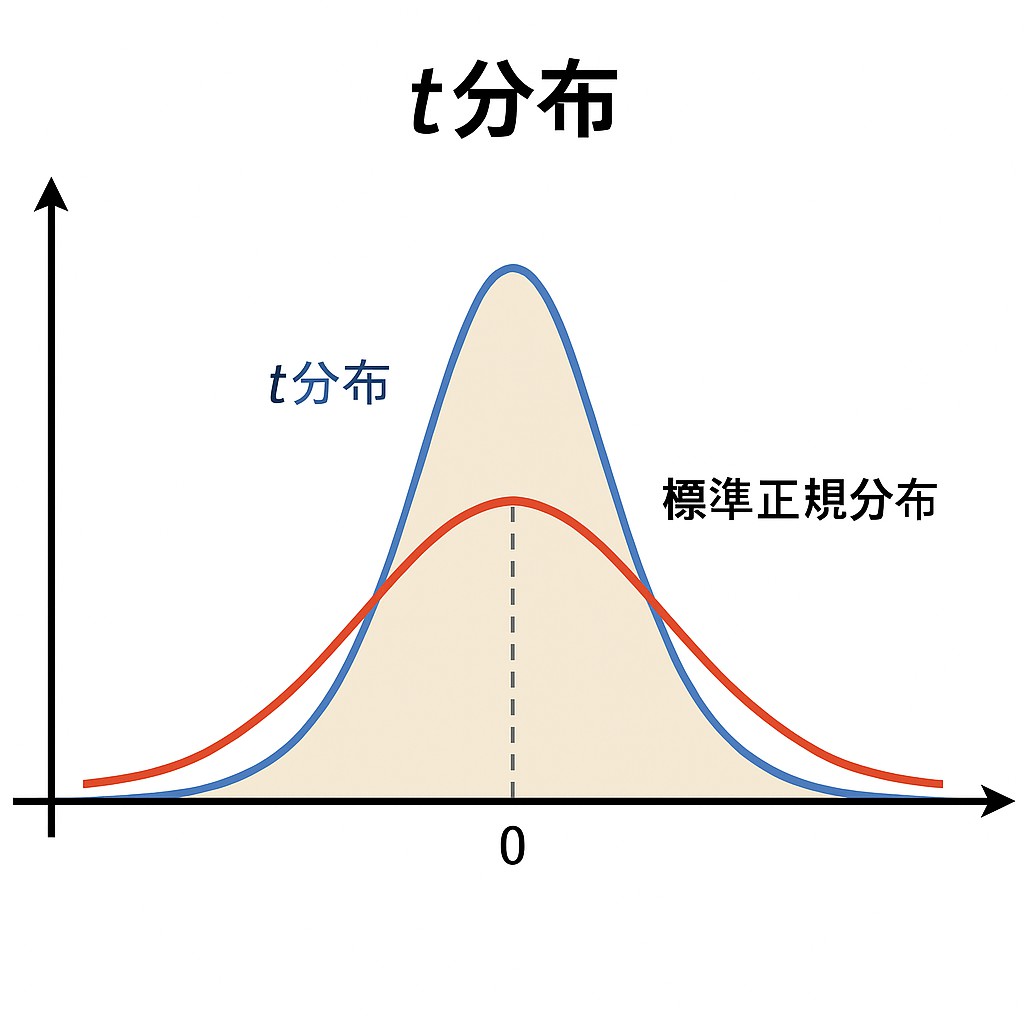
t検定を理解するうえで欠かせないのが「t分布」です。t分布とは、母分散が未知のときに、標本から計算された統計量(t値)が従う確率分布のことを指します。特に標本サイズが小さい場合に使われ、正規分布に似ていますが、裾がやや広く(分布の山が低く、両端が厚い)なっているのが特徴です。
この裾の厚さは「自由度」と呼ばれる値に依存し、自由度が増えるにつれてt分布は正規分布に近づいていきます。自由度が30を超えるころには、ほぼ標準正規分布と同じ形状になるため、大きなデータではt分布と正規分布をほぼ同じものとして扱うこともあります。
t検定では、このt分布を使って「得られたt値がどれだけ極端な値なのか(=母平均と本当に差があるのか)」を判断します。標本サイズが少ないときでも信頼できる判断ができるのが、t分布を使う最大の強みです。
統計学基礎参考情報
当サイトでは統計学の学習に役立つ情報を多数配信しております。是非以下のページをご覧ください。
統計学理論
統計学基礎から現場で使える実践的な内容に至るまで幅広く情報配信
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら

