【統計学基礎】母集団と標本

2025年5月4日

当ページには広告が含まれています。

こんにちは、DXCEL WAVEの運営者(@dxcelwave)です！

こんな方におすすめ

推定統計における母集団と標本の基礎について詳しく知りたい！

【推測統計】母集団と標本

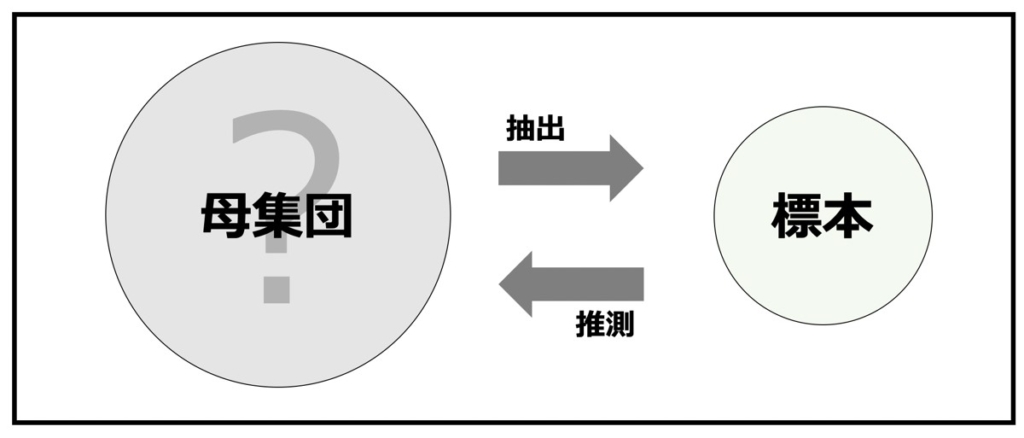
推測統計とは、データの一部を取り出してデータ全体について予測・判断するための手法です。

例えば、関東2,000万世帯の視聴率を1,000世帯の調査過程の視聴率から割り出したり、選挙結果を出口調査から予測したりするのが推定になります。

視聴率調査では対象である2,000万世帯全てを調査するのが理想です。これを全数調査（または悉皆調査）と言います。

一方、全数調査には費用がかかりすぎるため、一部を抜き出し1,000万世帯から全体の視聴率を予測することになります。

統計学ではこの2,000万世帯のような調査の対象となる集団を母集団（Population）と呼び、実際に調査する1,000万世帯を標本（Sample）と呼びます。

推測統計とは、母集団の分布の特徴を標本のデータから予測・判断することであるとまとめられます。

母集団と標本分布における基礎統計

母集団の平均を母平均、分散を母分散、標準偏差を母標準偏差と呼びます。これらのように、母集団の分布の特徴を表すパラメータを母数と呼びます。

母集団の分布を、母数（パラメータ）を用いたモデルで設定するとき、標本のデータから母数を推測することを推定と呼びます。

標本の平均を標本平均、標本の分散を標本分散、標本の偏差を標本標準偏差とと呼びます。

推定法

予測には2つあり、1つの値で予測することを点推定、範囲を持って予測することを区間推定と呼びます。なお、仮定した母数の値が正しいかどうか判断する手法を検定と呼びます。

標本の抽出法

標本抽出（Sampling）とは、母集団と標本のあいだにある関係を説明するためのものです。例えば日本国民全体を対象に、何か調査をするのは難しいですが、その中から、1000人だけを選んでアンケートを実施することは可能です。これが、母集団と標本の関係です。

無作為抽出と乱数

データ分析を行ううえで大切なのは、サンプル（標本）が元の集団（母集団）の特徴をきちんと反映していることです。そのために基本となる方法が無作為抽出（random sampling）です。これは、母集団の中から誰にでも同じ確率でサンプルを選ぶというやり方で、公平にデータを集めることができます。

たとえば箱の中にいろんな色のボールが入っている場合、目をつぶって1個取り出すようなイメージです。こうした実体がある場合は分かりやすいですが、コンピュータ上でこれを仮想的に行うには「乱数」が必要になります。

ただし、コンピュータは本当の意味で完全にランダムな数字を作り出すことができません。そこで使われるのが「疑似乱数」と呼ばれる、ランダムっぽく見える数字を生み出す仕組みです。実はこの疑似乱数にもいろいろなアルゴリズムがあり、Pythonをはじめとする多くのプログラミング言語やライブラリでは、「メルセンヌ・ツイスタ法（Mersenne Twister）」という手法が使われています。これは高速かつ質の高い疑似乱数を生成できることで、実用上ほとんどの用途に十分な精度を持っています。

復元抽出と非復元抽出

非復元抽出（sampling without replacement）は、一度取り出したサンプルを元の母集団に戻さない方法です。つまり、サンプルがどんどん減っていくので、取り出せるデータの数には限りがあるということになります。

これに対して、復元抽出（sampling with replacement）は、取り出したものを毎回母集団に戻すスタイルです。そのため、何回でも同じ条件で抽出ができる＝理論的には無限にサンプルが取れる、というイメージになります。

たとえばコイントスを考えてみましょう。裏か表のどちらかが出ますが、何度でも繰り返せるので、実質的にいくらでもサンプルを増やすことができます。復元抽出はまさにこのコイントスのように、繰り返しが可能な場面で使われる考え方です。

標本の抽出法（単純無作為抽出法・系統抽出法・二段抽出法・層化抽出法）

母集団の中の要素に番号を振って、サイコロや乱数表などを使い、ランダムに番号を選んでサンプルを取り出す方法は「単純無作為抽出法」と呼ばれます。とても基本的な手法で、まさに「ランダムに選ぶ」ことをストレートに実現する方法です。

一方、最初の1つを無作為に選んで、そこから一定の間隔ごとにデータを取り出していく方法は「系統抽出法」と呼ばれます。例えば、名簿の中で1人目をランダムに決めて、そこから10人おきに選んでいくようなやり方です。

もう少し複雑な方法に「二段抽出法」があります。たとえば、全国の世帯を対象に調査をしたいとき、まず市町村をランダムに50か所選び（これが第一抽出単位、いわゆる“クラスター”）、その後、各市町村の中からさらに30世帯ずつサンプルを選ぶ（これが第二抽出単位）といった具合です。エリアが広い場合や現地調査が必要な場面で、コストを抑えつつ代表性を保ちたいときによく使われます。

さらに、母集団をいくつかのグループ（層）に分けて、それぞれのグループからサンプルを取り出す方法を「層化抽出法」といいます。たとえば都道府県ごとにデータを取り、あとからそれを全体としてまとめる場合などがこれにあたります。地域や年齢、性別など、特定の属性ごとにバランスよくデータを集めたいときに有効な方法です。

標本分布の基礎統計

標本分布で扱う基礎統計について言及します。

標本分布の平均

Np個の母集団から、N個のサンプルを抽出したとします。（Np>N ）

N個の値の平均値という新しい確率変数xを考えます。このxの平均と、標準偏差は、母集団の平均と標準偏差を使って、次のように書くことができます。

平均: μ_x=μ

標準偏差: σ_x=σ/√N‾‾

これは、標本の統計量から、母集団の統計量を推し量ることができることを意味します。Nを大きくすればするほど、xの分散は小さくなるので、正確な平均値を知ることが出来るわけです。

比率の標本分布

成功確率p（失敗はq=1-p）で表現される母集団からの標本を考えます。N個のサンプルの平均という新しい確率変数を考えると、この平均と標準偏差は、次のように記載できます。

平均: μ_p = p

標準偏差: σ_p=√pq/N = √p(1−p)/N

標本の差と和

正規分布に従う2つの母集団 N1とN2があるとします。これらの母集団からの標本について、その差と和を考えて見ます。 S1をN1の統計量、S2をN2の統計量とすると、次の関係が成り立ちます。差の統計量については、

平均: μ_S1−S2=μ_S1−μ_S2

標準偏差: σ_S1−S2 = √σ²_S1+σ²_S2

和の統計量については、

平均: μ_S1+S2=μ_S1+μ_S2

標準偏差: σ_S1+S2 = √σ²_S1+σ²_S2

平均は分かり易いですが、標準偏差はどちらもおなじく、増大していることに注意してください。

信頼区間

信頼区間とは、統計分布の仕組みを使って、標本データから母集団の平均がどの範囲にあるかを確率的に示す方法です。たとえば、標本調査を行った結果、ある数値の平均が75だったとします。このとき「この75という数字が、本当に全体（母集団）の平均を表しているのか？」という疑問に対して、どの程度の範囲でその母平均が存在しそうかを示すのが信頼区間です。

たとえば「信頼水準95%の信頼区間を設定する」というのは、「同じような調査を100回やったら、そのうち95回はこの範囲の中に母平均が入るはずだ」と言っているのと同じです。具体的には、下限70から上限80の間に母平均が入る確率が95%と考えるわけです。同じ考え方で、信頼水準99%の信頼区間なら、100回中99回はその範囲に母平均が含まれると判断します。

つまり信頼水準95%というのは、誤差5%は許容している、という意味になります。信頼水準が高いほど確実性は増しますが、その分信頼区間の幅は広くなります。逆に信頼水準を下げれば、区間は狭くなるものの、確実性は下がるというトレードオフがあるのです。