こんにちは、DXCEL WAVEの運営者(@dxcelwave)です!
本記事と確率統計学における「条件付き確率」と「ベイズの定理」について詳しく解説しています。
また、上記の理解促進のため「事象と確率」についても概説しています。
事象と確率
事象
サイコロ投げのように、同じ条件のもとで何回も繰り返すことができ、その結果が偶然によって決まる観察や結果を試行といい、試行の結果起こる事柄を事象と呼びます。ある試行Tについて、起こりうる事象全体をUで表した時、Uで表される事象を全事象、空集合で表される事象を空事象と呼びます。
Uが有限個の要素を持つ場合、全ての事象はUの部分集合になります。例えば、サイコロの目が出る事象全体Uがある時、「1, 2, 3のどれかが出る事象」や「1の目が出る事象」というように分解が可能な事象があります。前者のように、分解が可能な事象を複合事象と言い、後者のこれ以上分解できない事象を根元事象と言います。さらに、どの根元事象も同程度に起こると期待できるとき、同様に確からしいと言います。
確率
根元事象が同様に確からしいという仮説のもとで、事象Xの確率は次のように表されます。

(例)2つのサイコロの和が9になる確率
2つのサイコロの合計が9になる場合の数:(3,6), (4,5), (5,4), (6, 3) ⇨ 4パターン
全事象:6 × 6 = 36パターン
2つのサイコロの合計が9になる確率 = 4/36 = 1/9
ベン図と和事象・積事象・余事象
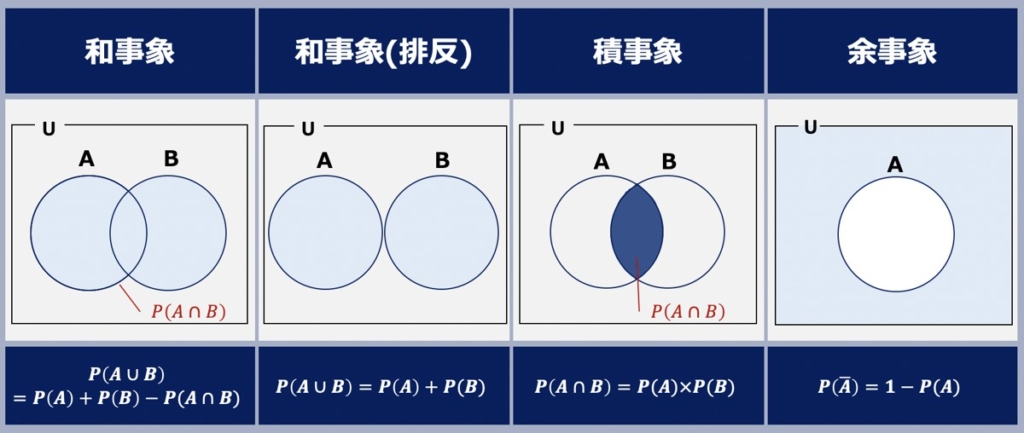
A∪Bと表記する和事象は「AまたはBが起こる」という事象です。AとBが同時に起こらないとき、AとBは排反である、もしくは排反事象であると言います。
A∩Bと表記する積事象は「AとBがともに起こる」という事象を指します。
全事象Uの中でAが起こらないという事象を余事象と言います。
独立事象と同時確率

AとBの2つの事象があり、A、Bの確率的な状況が互いに無関係、すなわちお互いの結果に影響しあうことが無い場合、AとBは独立といいます。
AとBが独立であるとき、AとBは上記のような積で表すことができます。
条件付き確率とベイズの定理
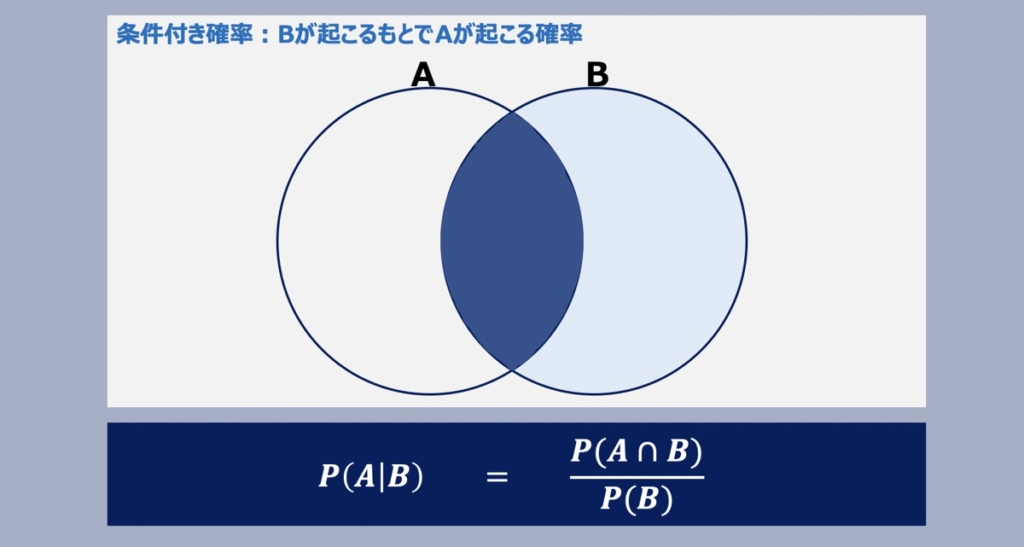
条件付き確率
条件付き確率とは、事象Aが発生した場合に事象Bが発生する確率です。P(A|B)として表されます。
P(A|B)はベン図で言えば、水色部分(B)を1とした時の網目部(A∩B)の割合です。
すなわち、P(B)を1としてみた時のP(A∩B)の割合を示しています。普通の確率では全事象Uを1として計算しますが、条件付き確率P(A|B)では、Bを言わば全事象と見て確率を計算するのです。
条件付き確率を活用した事例
| 趣味 | 10代 | 20代 | 合計 |
|---|---|---|---|
| 野球観戦 | 10 | 25 | 35 |
| サッカー観戦 | 20 | 5 | 25 |
| 合計 | 30 | 30 | 60 |
年齢20〜30代を60人を対象に、スポーツ観戦の趣味について聞いたところ、上記結果が得られたとします。また、60人から無作為に1人を選んだ時のことを考えます。
選ばれた人が野球観戦が好きである確率は、35/60であることが分かります。ここで、もしも選ばれた人が10代であるという情報が事前に与えられたとしましょう。これは、10代であるという条件が付与されたことを意味しますので、表の10代の列に着目し、確率を計算すると良いことになります。従って、確率は10/30です。
選ばれた人が10代であるという条件のもと野球観戦が好きである確率、これこそが条件付き確率になります。
ベイズの定理
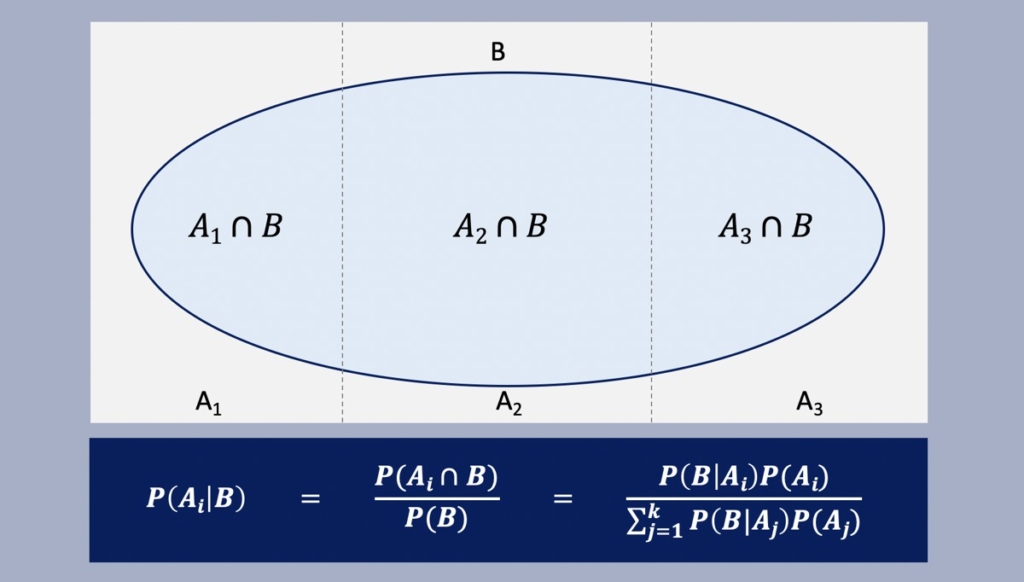
事象Bが起こるという条件のもとで、k種類の事象Ai(A1, A2, A3・・・Ak)が起こるとします。このとき、事象Bが起こるという条件のもとで、事象Aiが起こる条件付き確率P(Ai|B)は次のように表されます。
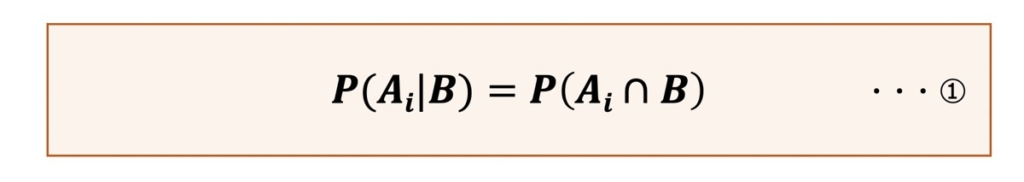
ここで確率の乗法定理は次のように表されます。
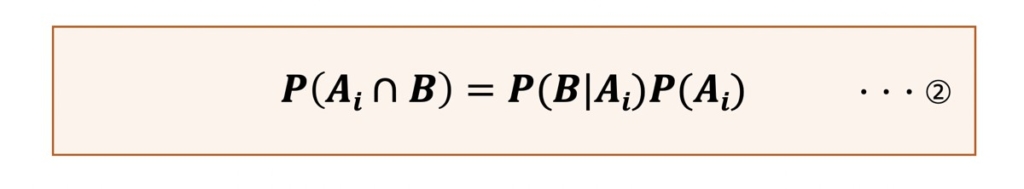
①に対して②を代入すると、次のような式が得られます。これがベイズの定理を指します。
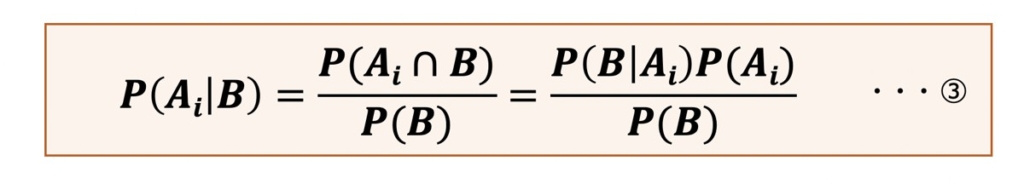
ここで全事象UがA1, A2, A3に割られている場合、 P(A2|B)は次のように表されます。
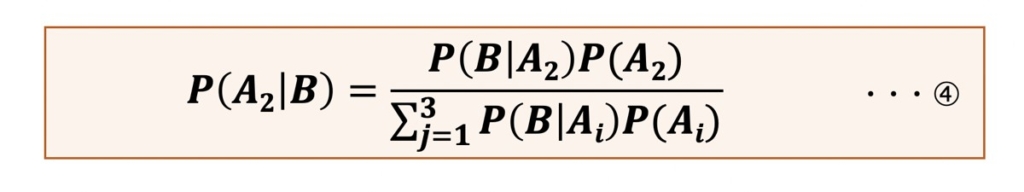
このように、他事象の確率の和や積を求めることで、目的の条件付き確率を求めることが可能です。この
【参考】統計学の学習におすすめな教材
「データ分析する上で統計学の基礎を学びたい」方向けに以下の教材をおすすめします。
統計学基礎参考情報
当サイトでは統計学の学習に役立つ情報を多数配信しております。是非以下のページをご覧ください。
統計学理論
統計学基礎から現場で使える実践的な内容に至るまで幅広く情報配信
最後に

お問い合わせフォーム
上記課題に向けてご気軽にご相談下さい。
お問い合わせはこちら


